Texas Instruments TI-82

35
G
RAPHING
T
ECHNOLOGY
G
UIDE
: TI-82
Copyright © Houghton Mifflin Company. All rights reserved.
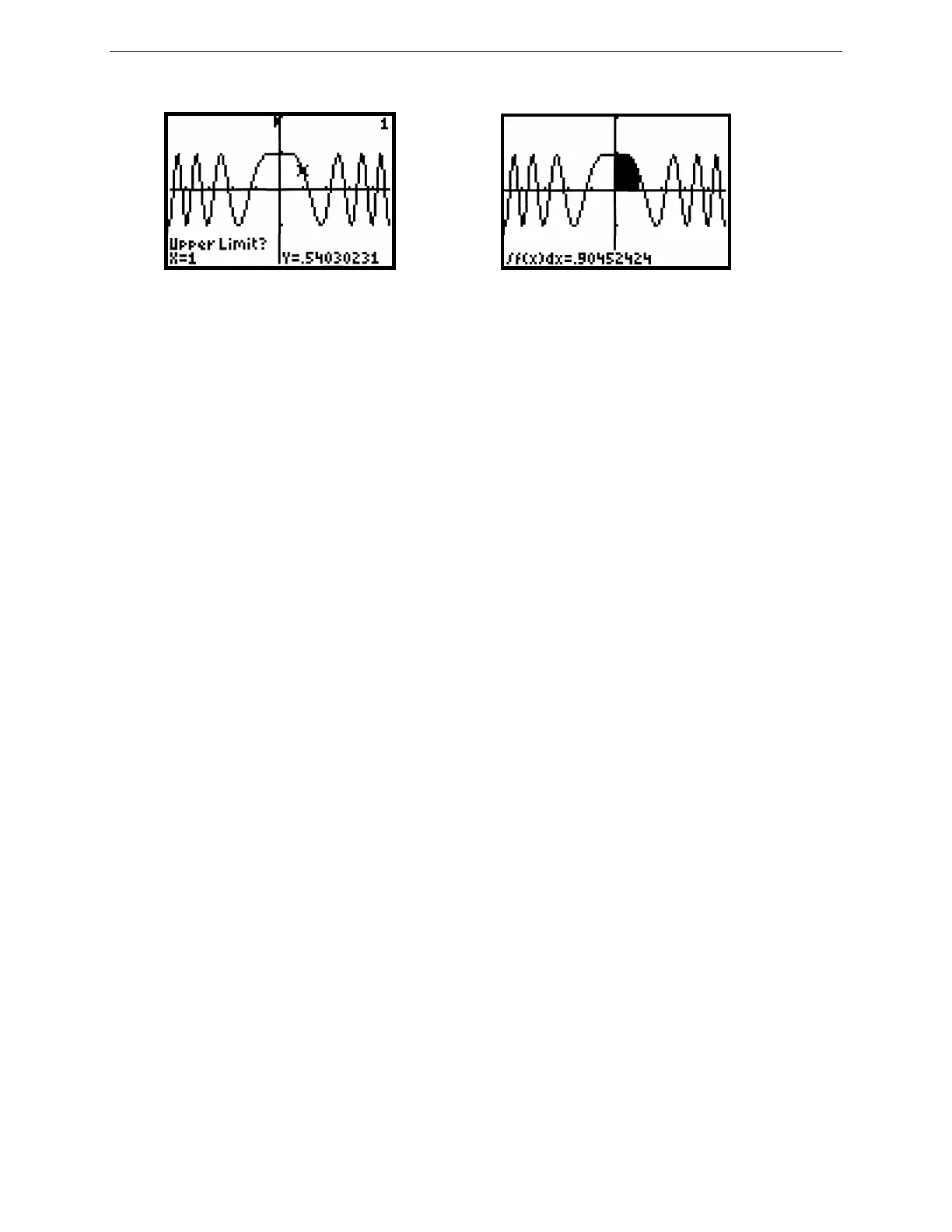
Figure 2.87: Setting the upper limit Figure 2.88:
∫
f(x)dx
Technology Tip: When approximating the area under f (x) = cos x
2
between x = 0 and x = 1, you must trace along
the curve to exactly where x = 0 and x = 1. Now to trace along the curve to x = a, the viewing rectangle must be
chosen so that the function is evaluated at x = a. The window shown in Figure 2.87 was made first by pressing
ZOOM 4 [Zdecimal], then by changing its vertical dimensions to appropriate values. By contrast, find the area
under f (x) = cos x
2
between x = 0 and x = 1 in ZOOM 7 [Ztrig] window.
Technology Tip: Suppose that you want to find the area between two functions, y = f (x) and y = g(x), from x = A to
x = B. If f (x)
≥
g(x) for A
≤
x
≤
B, then enter the expression f (x) – g(x) for Y
1
and proceed as before to find the
required area.