4. Calculation of wavelength for any colour
The images to left and right of the central
vertical line of LEDs are called first order
fringes. If you look again and hold the
grating close to your eye, you should see
a second set of images, fainter and further
out from the vertical centre line. These are
second order fringes.
By making simple measurements, you can
calculate the wavelength of the light
emitted by each LED.
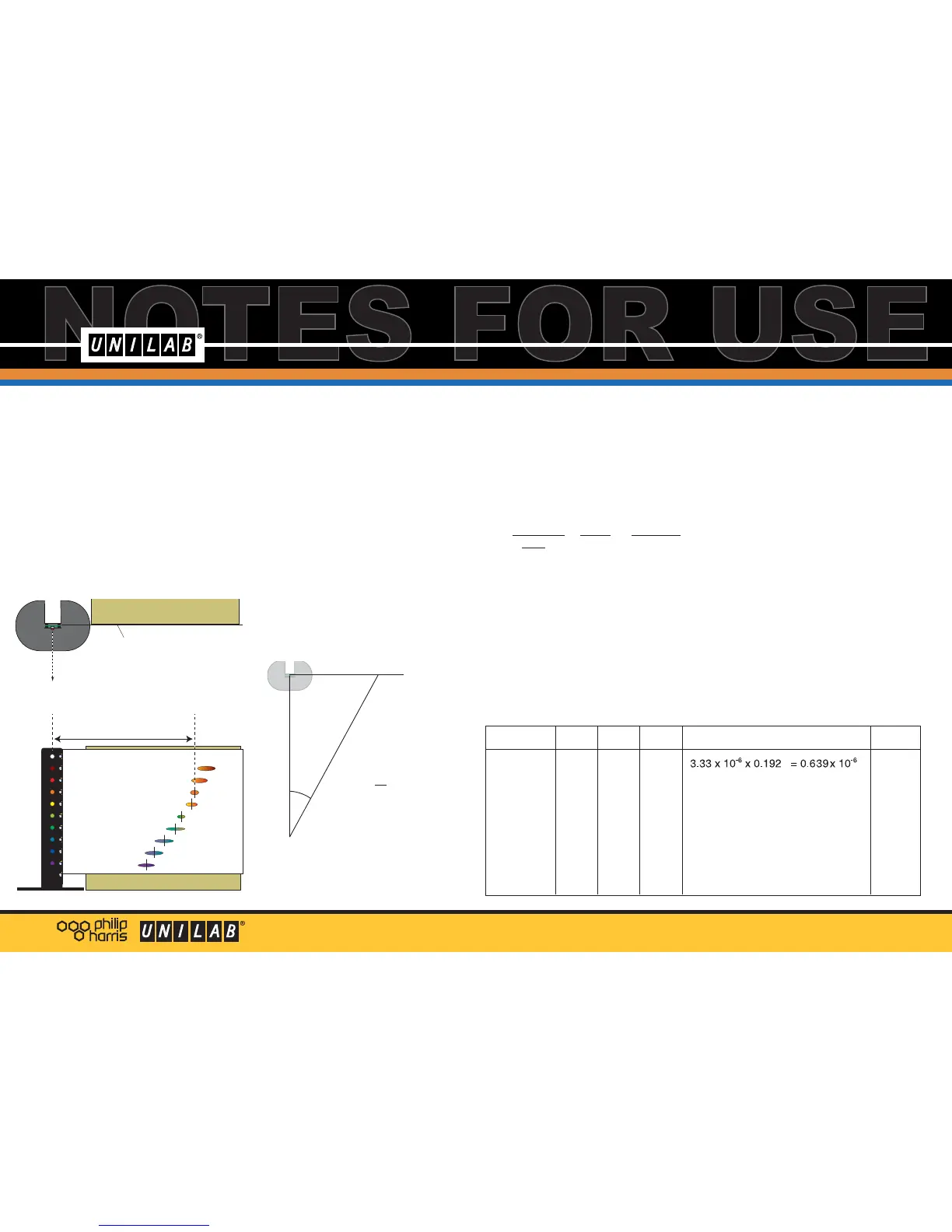
Support a sheet of A3 card or paper,
vertically, to one side of the LED array, this
can be done using blu tac and a box.
Now face the LED array, with the
diffraction grating 1 metre from the array,
and close to your eye. Arranging the
grating in a clamp stand might help you fix
the distance accurately.
The A3 card should be at right angles to
the line from your eye to the array.
As you look through the grating, guide
another student to mark the centre of each
first order image, using a marker pen.
Without disturbing the card, measure the
distance,
y, from the centre line of the LED
array to each mark in turn, in metres.
Note the LED colour and the distance,
y.
For each LED, calculate tan
θθ
in this case x = 1 metre
Use a scientific calculator (or the Windows
Calculator accessory) to find the angle
θθ
using the tan
-1
or “Inv tan” function.
Then find sin
θθ
and enter it in the table.
In the formula m
λλ
= d sin
θθ
m = 1 for a first order fringe
λλ
= the wavelength of light from the LED
d = the spacing of the lines in the grating,
in metres.
For a 300 line/mm grating this is
1
= 1mm = 10
-3
metre
300 300 300
1mm
= 0.00333 x 10
-3
d = 3.33 x 10
-6
m
So, for each LED
λλ
= 3.33 x 10
-6
x sin
θθ
A typical result has been entered for the
deep red LED.
Measure
y for the rest of the LEDs,
calculate and enter the wavelength in the
table.
Units
Your wavelength values in the table were
calculated as 0.574 x 10
-6
metre, for
example.
Wavelengths of light are usually quoted in
nanometres (nm), and that value would
become 574 nm.
1 nanometre is 10
-9
or 1 thousand
millionth of a metre. Visible light has
wavelengths in the range 400 to 700nm,
for a typical human eye.
Errors
The quoted wavelength for the deep red
LED is 641 nanometres.
The value 639nm is quite close, within
0.5% in fact.
What are the likely sources of error in
wavelength values measured in this way?
How can you change the method to give
even more accurate values?
 Loading...
Loading...