Casio fx-3650P

30
21 The sum, difference and inner
product of two vectors
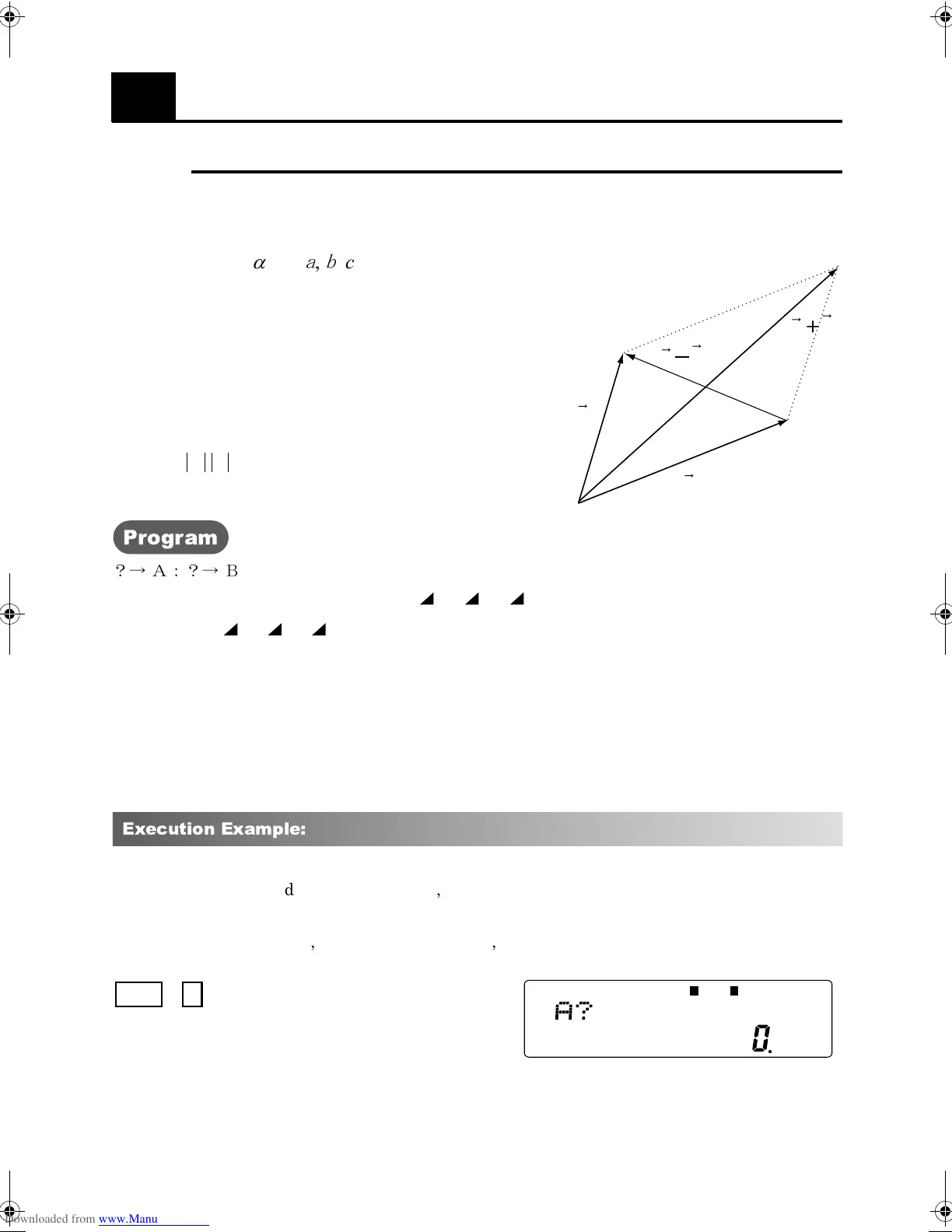
The sum and difference of two vectors in 3-dimensional space is obtained by adding and
subtracting their respective components.
For example, for , ,
The inner product is defined:
Program
？→ Ａ：？→ Ｂ：？→ Ｃ：Ａ → Ｘ：Ｂ → Ｙ：Ｃ → Ｍ：？→ Ａ：？→ Ｂ：？→ Ｃ：Ａ ＋ Ｘ
→ Ａ：Ｂ ＋ Ｙ → Ｂ：Ｃ ＋ Ｍ → Ｃ：Ａ Ｂ Ｃ ２Ｘ－Ａ→Ａ：２Ｙ－Ｂ→Ｂ：２Ｍ
－Ｃ→Ｃ：Ａ Ｂ Ｃ （Ｘ － Ａ）Ｘ＋（Ｙ－Ｂ）Ｙ＋（Ｍ － Ｃ）Ｍ → Ｄ：Ｄ ＜ 111 STEP ＞
INPUT Ａ,Ｂ,Ｃ(first time) : Ａ,Ｂ,Ｃ(second time):
OUTPUT Ａ,Ｂ,Ｃ(first time) : sum of two vectors
Ａ,Ｂ,Ｃ(second time): difference of two vectors
Ｄ : inner product
Execution Example:
For and ,
, ,
α ab c,,()=
→
β a ′ b ′ c′,,()=
→
β
β
α
α
β
α
αβ + abc,,()a′ b′ c′,,()+ aa′+ bb′+ cc′+,,()==
→
→
αβ – abc,,()a′ b′ c′,,()– aa′– bb′– cc′–,,()==
→
→
αβ ⋅ α
β
θ cos aa′ bb′ cc′++==
→
→
→
→
α abc,,()=
→
β a ′ b ′ c ′ ,,()=
→
αβ ⋅
→
→
α 1 23,,()=
→
β 28 3–,,()=
→
αβ + 3 100,,()=
→
→
αβ – 1– 6– 6,,()=
→
→
αβ ⋅ 9=
→
→
Prog
1
S A
D R P1
P1
P2 P3 P4 G
関数電卓事例集 .book 30 ページ ２００２年９月２日 月曜日 午後６時５１分