Casio fx-3650P Programming Guide

33
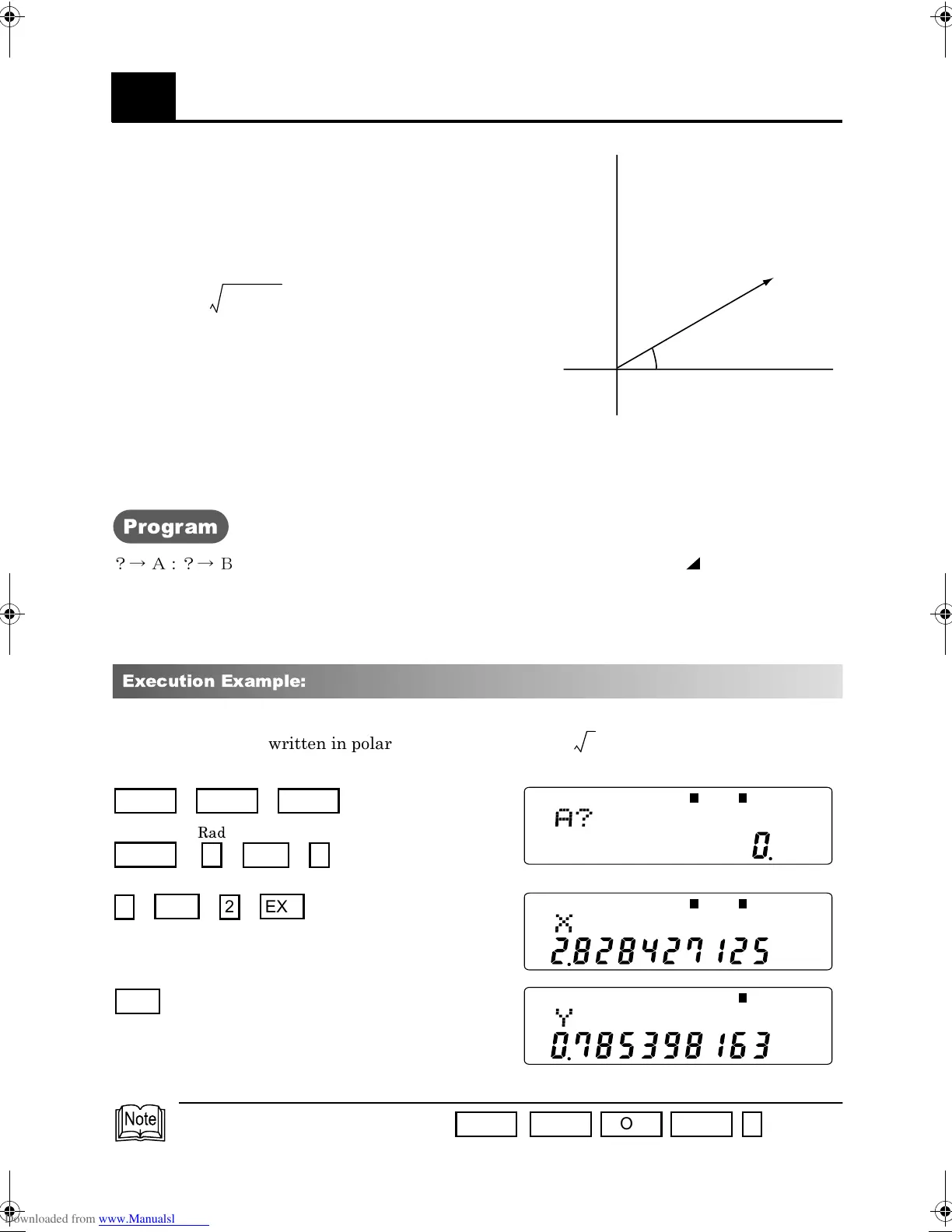
23 Complex numbers and polar coordinates
As an example, for the complex number ,
we may write in polar coordinates, by letting
=
where .
The product of two complex numbers in polar form is
.
Program
？→ Ａ：？→ Ｂ：√（Ａ
２
＋Ｂ
２
）→ Ｘ：ｃｏｓ
－１
（Ａ ÷ Ｘ）→ Ｙ：Ｘ Ｙ ＜ 31 STEP ＞
INPUT A : real part
a B : imaginary part b
OUTPUT X : the distance from the origin Y : the angle
from the real line
Execution Example:
, when written in polar coordinates is .
To obtain the answer in degrees, press before
executing the program.
ω abi+=
ω
ω r θ cos i θ sin+()
a + bi
θ
r
ra
2
b
2
+ θ cos
a
r
---= θ sin
b
r
---=,,=
r θ cos i θ sin+()r′ θ cos i θ ′sin+()× rr′ θθ′ +()cos i θθ′ +()sin+()=
θ
ω
22i+= ω 22
π
4
---cos i
π
4
---sin+


=
MODE MODE MODE
MODE
2
Rad
Prog
1
S A
D R
P1
P1
P2 P3 P4 G
2
EXE
2
EXE
Disp
S A
D R P1
P1
P1
P1
P2 P3 P4 G
8
EXE
S A
D R P1
P1
P2 P3 P4 G
MODE MODE MODE MODE
1
関数電卓事例集 .book 33 ページ ２００２年９月２日 月曜日 午後６時５１分

Casio fx-3650P Specifications

General

Type	Scientific
Form factor	Pocket
Housing material	Plastic
Digits	12 digits
Digit comma separator	Yes
Display number of lines	2 lines
Digit comma separator format	Standard (3 digits)
Battery type	LR44
Number of batteries supported	1

Weight and Dimensions

Weight	100 g
Dimensions (WxDxH)	78 x 157 x 12 mm