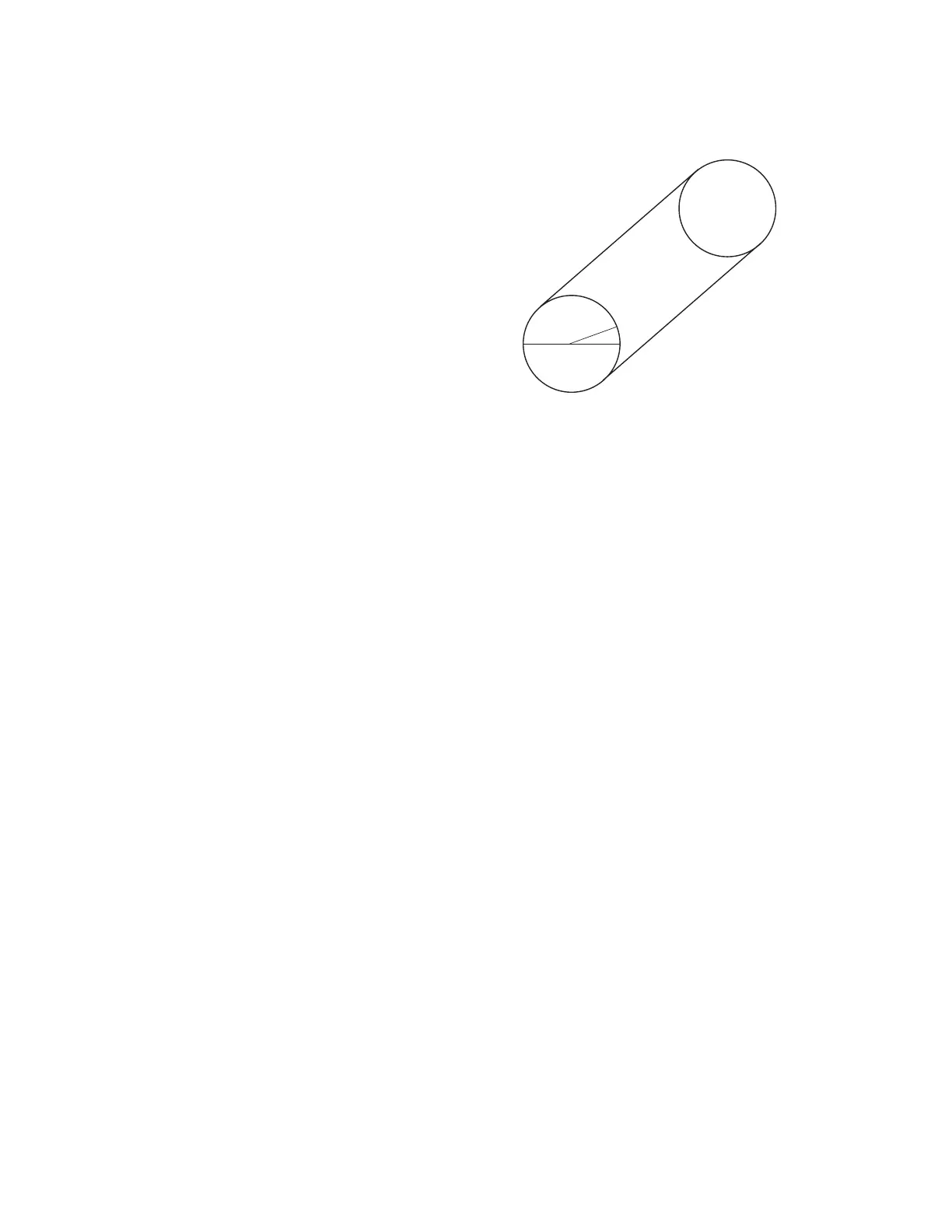
Let’s break it down. First you will need to know the port’s dimensions. Let’s use a 12” long port with a 2”
diameter. Now we need to calculate the area of a circle the same size as the port, 2” in this case. ARGH!
Here comes that Geometry stuff again! The area of a circle is the radius squared multiplied by “pi” ( “pi” is
cool, he he.) or 3.14”.
In case you were wondering, the radius is half of the diameter for all those who slept
through Geometry!
Area of a Circle = r
²
x 3.14
The radius of our circle is 1”
1² x 3.14 = 3.14”
Next, we’ll multiply this by the ports length, 12”.
12” x 3.14” = 37.68 cu. in.
So, to get the accurate volume of the enclosure,
we’d need to deduct 37.68 cu. in. from the total volume.
Brace Displacement: After figuring port displacement, brace displacement is relatively easy. Braces are
discussed in detail a little later so trust us for now. We’ll use a 1” x 1” x 20” brace for an example. All we do
is multiply the dimensions together(1” x 1” x 20” = 20 cu. in.) and deduct this amount from the cabinet’s
total volume. Piece of cake, Joey! Remember to do this for all braces in the enclosure, there may be quite a
few of them!
Driver Displacement: The driver also takes up air space inside the enclosure. If you use Kicker speakers,
we’ve made calculating driver displacement real simple for you, just flip to the chart on page 14 of this sec-
tion. The recommended enclosure volumes we give in this manual already have the driver displacement
deducted. If you do the intelligent thing and use our speakers, you won’t have to figure driver displace-
ment. We have a staff of engineers, whom we lock away in a special hermetically sealed room in order to
calculate driver displacement. Depending on how many new models we release, they may not see the light
of day for months. Let’s revisit the example, shall we. We currently have 1.79 cu. ft. per driver before dis-
placement. This size box might work for a 12” driver or a 10’ driver.. Let’s calculate driver displacement now
to where we are now.
12” driver displacement = 0.070 cu. ft. 1.79 - .070 = 1.72 cu. ft. per 12”
10” driver displacement = 0.044 cu. ft. 1.79 - .044 = 1.746 cu. ft. per 10”
Now we’ll look at braces. Two different types of braces are corner braces and cross braces. For this exam-
ple, we are building a sealed enclosure in a simple rectangular box. We’ll have twelve corner braces( one for
each joint), and six cross braces (one for each wall).
We have eight corner braces that are 1” x 1” x 12.5”. Each one uses 12.5 cu. in. of our enclosures total
volume, so eight of them use : 8 x 12.5” = 100 cu. in.
Four corner braces are 1” x 1” x 37.5”. We deducted two inches from the length so the braces would
meet instead of overlap the other corner braces. Each one of these uses 37.5 cu. in. of our volume, so
multiply this figure by four = 4 x 37.5” = 150 cu. in.
 Loading...
Loading...