FUNS
The FUN Equations
16-8
hipass (f = a, b)
With this equation the low values of input b are filtered according to the value of input a. This
causes somewhat different results compared with the lowpass equation above. At low values
for input a, low values for input b will have little effect, while high values for input b will
cause the FUN to quickly reach full effect then slowly sweep down to its starting level. At high
values for input a, a rapid change in the value of input b will have little effect. At low values for
input a, rapid changes in the value of input b will cause the FUN to respond quickly to the
change, then slowly fade back to minimum effect. Listening to the effects at different values for
each input will give you the best understanding.
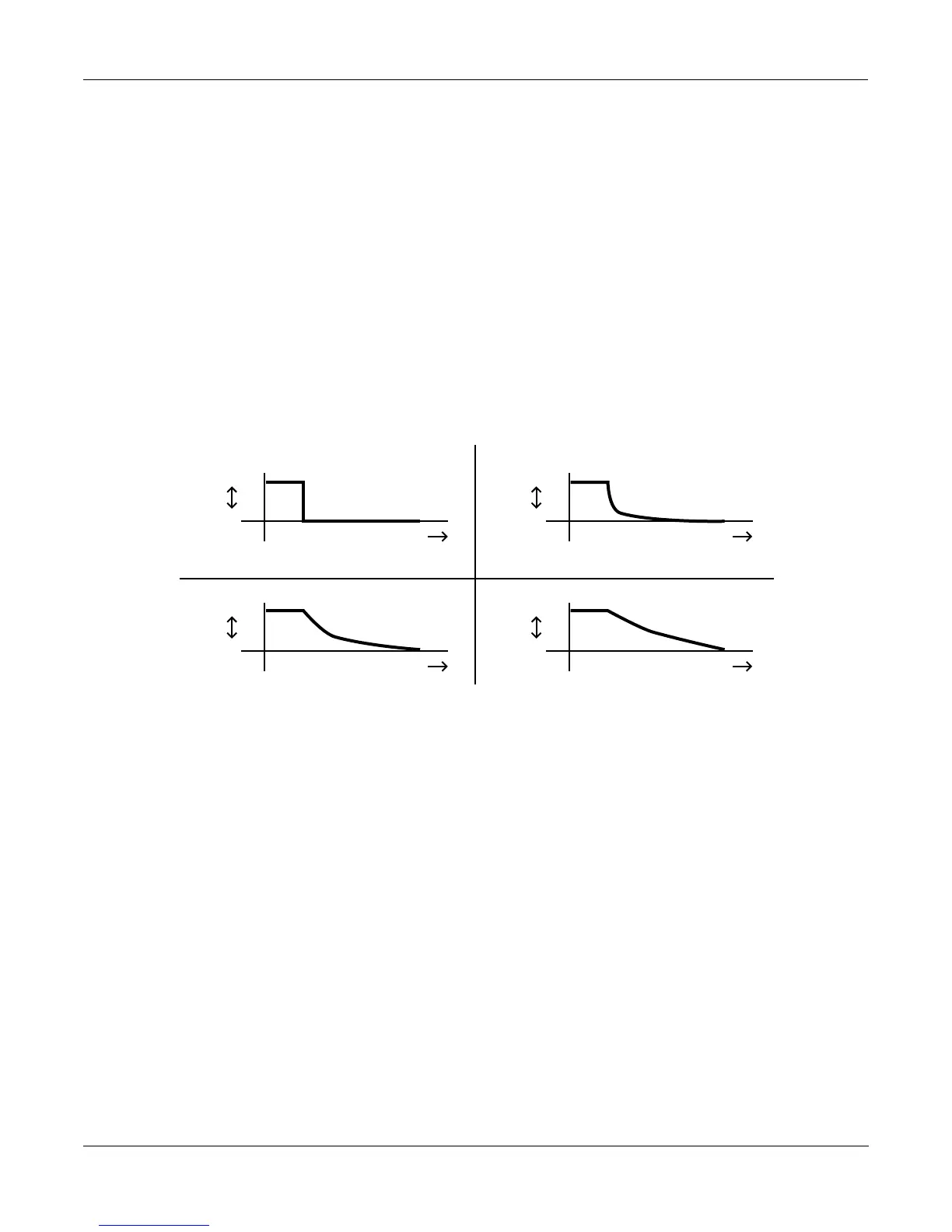
The four graphs below show the effect of different values for input a on the change of input b.
In each graph, the value of input b drops from +1 to 0. In graph 1, the value of input a is +1.
Each successive graph represents the same change in the value of input b, at successively lower
values for input a.
b / (1 - a)
This is another weighted difference equation similar to the first six. The value of input a is
subtracted from 1. The value of input b is then divided by the difference. You’ll get
considerably different results for different input values of a and b.
a(b-y)
Think of this equation as reading “y is replaced by the result of the function a(b-y).” The value
of y indicates the value of the FUN’s output signal. Every 20 milliseconds, the K2500 takes the
current value of y, runs the equation, calculates a new value of y, and inserts the new value into
the equation. Consequently the value of y will change every twenty milliseconds. Here’s an
example. When you play a note, the K2500 starts running the FUN. The first value for y is
always 0. We’ll assume the value of input a is +.5, and the value of input b is +1. The first time
the K2500 evaluates the FUN, the result of the equation is .5 x (+1 - 0), or .5. So the FUN’s
output value after the first evaluation is .5. This becomes the new value for y, and when the
K2500 does its next evaluation of the FUN, the equation becomes .5 x (+1 - .5), or .25. The
resulting output value is .25, which becomes the new value for y. For the next evaluation, the
equation is .5 x (+1- .25), or .375.
(a + b)^2
The values of inputs a and b are added, and the result is squared (multiplied by itself). This will
change the linear curve of a unipolar control signal into a curve that’s lower at its midpoint (by
a factor of 2). Bipolar control signals will generate curves that are high at both ends, and 0 in the
middle.
1)
4)3)
2)
input b
value
time
input b
value
time
input b
value
time
input b
value
time

 Loading...
Loading...











