TI-89 Guide
TI89-25
Copyright © Houghton Mifflin Company. All rights reserved.
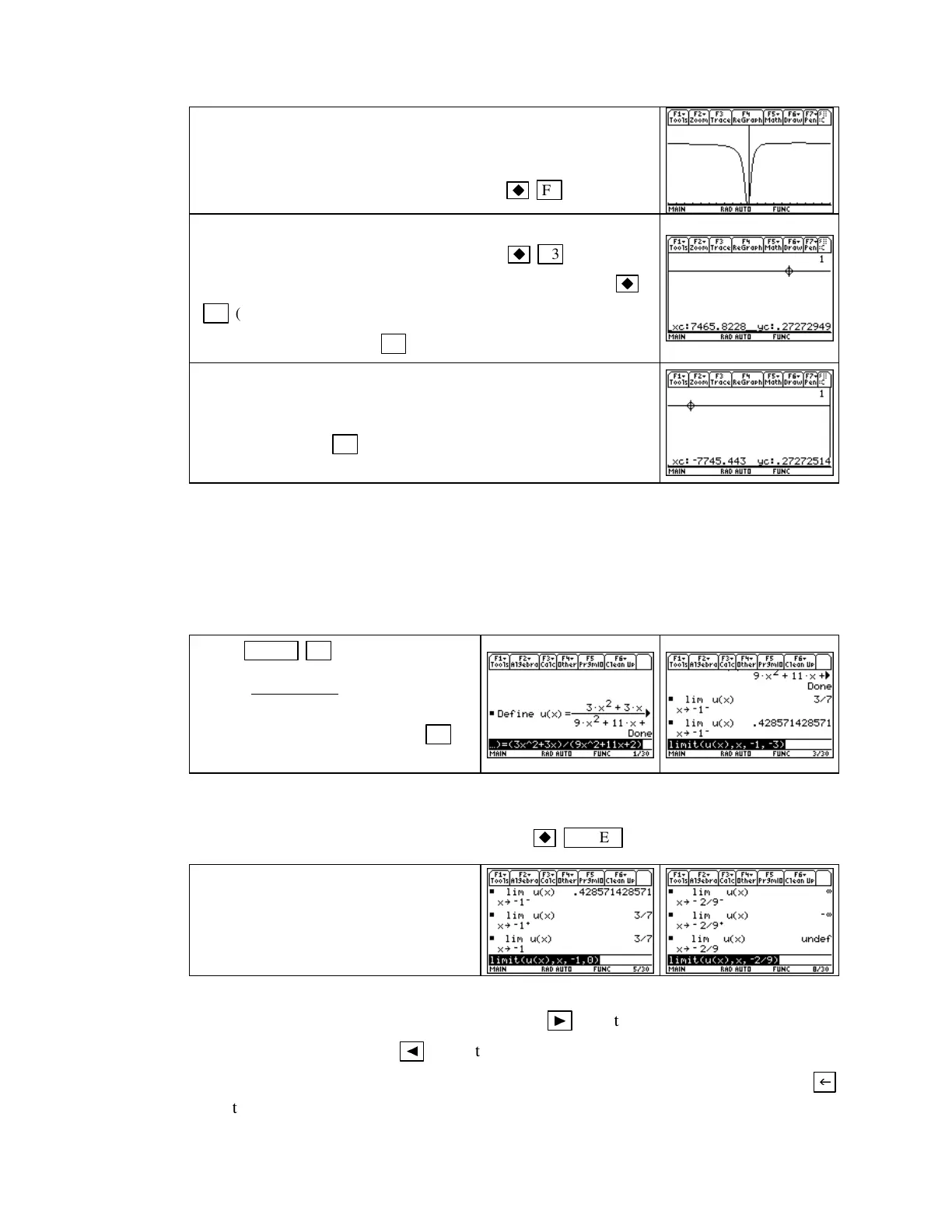
We estimated the limit as x gets very large or very small to be
0.273. Now, u(0) = 0, and it does appears from the graph that u
is never negative. Set a window with values such as
xmin =
−
10,
xmax = 10, ymin = 0,
and
ymax = 0.35.
Press
F3 (GRAPH).
To examine the limit as x gets larger and larger, change the win-
dow so that
xmax = 100,
view the graph with
F3 (GRAPH),
change the window so that
xmax = 1000,
view the graph with
F3 (GRAPH),
and so forth. The graph to the right was drawn
with
xmax = 10,000
.Use
F3 [Trace]
with each graph.
Repeat the process as x gets smaller and smaller, but change
xmin
rather than
xmax
after drawing each graph. The graph to the right
was drawn with
xmin =
−
9000, xmax = 10, ymin = 0,
and
ymax =
0.35.
Again, press
F3 [Trace]
on each graph screen to view some
of the outputs and confirm the numerical estimates.
1.4.5 FI NDI NG LI MI TS ALGEBRAI CALLY As previously mentioned, the TI-89 finds limits
algebraically. You can use this feature to confirm numerical and graphical estimates or use it as
a method of finding limits. The TI-89 syntax is
limit (function, input variable, point, direction).
For a limit from the left,
direction = any negative number
; for a limit from the right,
direction =
any positive number
; for a limit from both sides,
direction = 0
or
direction
is omitted from the
instruction. We illustrate using the function u that appears in Example 2 of Section 1.4.
Press
HOME F4 1[Define]
and type
u(x)=
33
9112
2
2
xx
xx
+
++
.Find
lim
x→
−
1
−
u(x).
Access the limit instruction with
F3
[Calc] 3 [limit(].
NOTE: We used
−
3 to indicate the direction in the limit statement. The TI-89 considers only
thenegativesign,soanynegativenumbergivesthesameresult–tryit! Alsorememberthatif
you want a decimal approximation for the answer,
ENTER
gives it.
Find
lim
x→
−
1
+
u(x),
lim
x→
−
1
u(x),
lim
x→
−
2/9
−
u(x),
lim
x→
−
2/9
+
u(x), and
lim
x→
−
2/9
u(x).
(See the note below for a shortcut.)
NOTE: Instead of retyping the limit statement each time to find the above limits, remember
that when the entry line is highlighted, you can press
►
to put the cursor on the right-hand
side of the statement and press
◄
to put the cursor on the left-hand side of the statement. The
statement is ready for editing using the arrow keys to move to the correct location and using
to delete unwanted symbols.

 Loading...
Loading...


















