11
Änderungen vorbehalten
Blindströme belasten das Stromversorgungsnetz.
Um die Blindleistung zu senken muss der Phasen-
winkel ϕ verkleinert werden. Da Transformatoren,
Motoren, etc. das Stromversorgungsnetz induktiv
belasten, werden zusätzliche kapazitive Widerstände
(Kondensatoren) zugeschaltet. Diese kompensieren
den induktiven Blindstrom.
Beispiel für Leistung mit Blindanteil
Bei Gleichgrößen sind Augenblickswerte von Strom und Span-
nung zeitlich konstant. Folglich ist auch die Leistung konstant.
Im Gegensatz dazu folgt der Augenblickswert von Misch- und
Wechselgrößen zeitlichen Änderungen nach Betrag (Höhe) und
Vorzeichen (Polarität). Ohne Phasenverschiebung liegt immer
die gleiche Polarität von Strom und Spannung vor. Das Produkt
von Strom x Spannung ist immer positiv und die Leistung wird
an der Last vollständig in Energie umgewandelt. Ist im Wech-
selstromkreis ein Blindanteil vorhanden ergibt sich eine Pha-
senverschiebung von Strom und Spannung. Während der Au-
genblickswerte in denen das Produkt von Strom und Spannung
negativ ist, nimmt die Last (induktiv oder kapazitiv) keine Lei-
stung auf. Dennoch belastet diese sogenannte Blindleistung
das Netz.
Scheinleistung (Einheit Voltampere, Kurzzeichen VA)
Werden die in einem Wechselstromkreis gemessenen Werte von
Spannung und Strom multipliziert ergibt das stets die Schein-
leistung. Die Scheinleistung ist die geometrische Summe von
Wirkleistung und Blindleistung.
Wenn: S = Scheinleistung
P = Wirkleistung
Q = Blindleistung
U
eff
= Spannung Effektivwert
I
eff
= Strom Effektivwert
ergibt sich für die Scheinleistung
S = P
2
+ Q
2
= U
eff
x J
eff
3.7 Leistungsfaktor
Der Leistungsfaktor PF (power factor) errechnet sich nach der
Formel:
PF = Leistungsfaktor
S = Scheinleistung
P = Wirkleistung
û = Spannung Spitzenwert
î = Strom Spitzenwert
Nur für sinusförmige Ströme und Spannungen
gilt: PF = cos ϕ
P
PF = ——
S
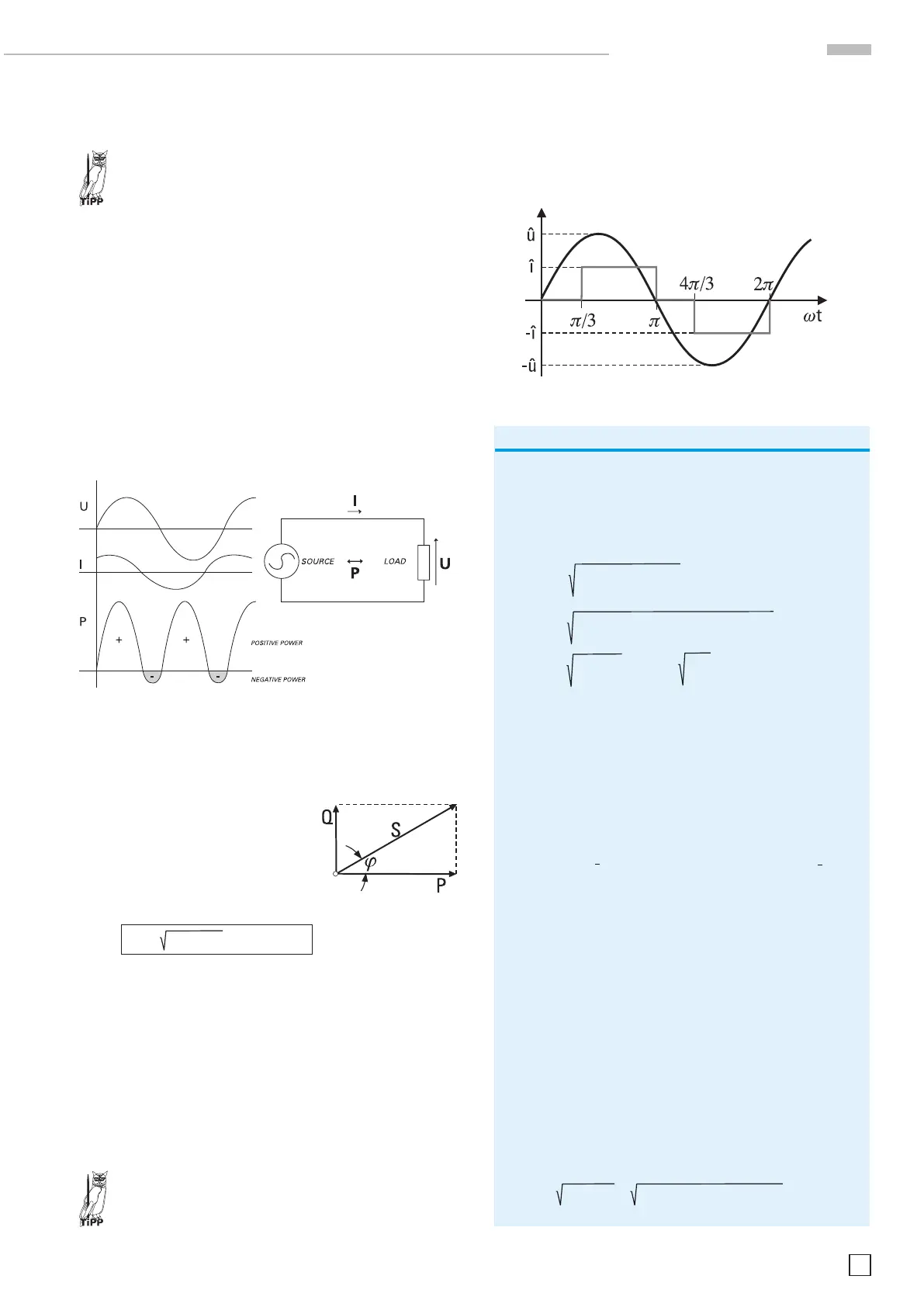
Ist zum Beispiel der Strom rechteckförmig und die Spannung
sinusförmig errechnet sich der Leistungsfaktor aus dem Ver-
hältnis von Wirkleistung zu Scheinleistung. Auch hier lässt sich
eine Blindleistung bestimmen. Aufgrund dessen, dass der
Strom eine andere Kurvenform besitzt als die Spannung, nennt
man diese Blindleistung auch Verzerrungsblindleistung.
û = 325,00 V; î = 12,25 A
Messgrundlagen Messgrundlagen
Rechenbeispiel Leistungsfaktor
Der Effektivwert der Spannung beträgt:
Der Effektivwert des Stromes ergibt sich aus:
Die Scheinleistung S entspricht:
S = U
eff
· I
eff
= 230 V · 10,0 A = 2300 VA
Die Wirkleistung errechnet sich aus:
Der Leistungsfaktor PF berechnet sich aus:
Strom und Spannung sind in unserem Beispiel nicht pha-
senverschoben. Dennoch muss es eine
da die Scheinleistung größer als die
Strom eine andere Kurvenform als die Spannung besitzt,
spricht man davon, dass der Strom gegenüber der Spannung
„verzerrt“ ist. Deshalb heißt diese Art von
„Verzerrungsblindleistung“.
Blindströme belasten das Stromversorgungsnetz.
Um die Blindleistung zu senken muss der Phasen-
winkel ϕ verkleinert werden. Da Transformatoren,
Motoren, etc. das Stromversorgungsnetz induktiv
belasten, werden zusätzliche kapazitive Widerstän-
de (Kondensatoren) zugeschaltet. Diese kompensie-
ren den induktiven Blindstrom.
Beispiel für Leistung mit Blindanteil
Bei Gleichgrößen sind Augenblickswerte von Strom und Span-
nung zeitlich konstant. Folglich ist auch die Leistung konstant.
Im Gegensatz dazu folgt der Augenblickswert von Misch- und
Wechselgrößen zeitlichen Änderungen nach Betrag (Höhe) und
Vorzeichen ( Polarität). Ohne Phasenverschiebung liegt immer
die gleiche Polarität von Strom und Spannung vor. Das Pro-
dukt von Strom x Spannung ist immer positiv und die Leistung
wird an der Last vollständig in Energie umgewandelt. Ist im
Wechselstromkreis ein Blindanteil vorhanden ergibt sich ei-
ne Phasenverschiebung von Strom und Spannung. Während
der Augenblickswerte in denen das Produkt von Strom und
Spannung negativ ist, nimmt die Last ( induktiv oder kapazitiv)
keine Leistung auf. Dennoch belastet diese sogenannte Blind-
leistung das Netz.
Scheinleistung (Einheit Voltampere, Kurzzeichen VA)
Werden die in einem Wechselstromkreis gemessenen Wer-
te von Spannung und Strom multipliziert ergibt das stets die
Scheinleistung. Die Scheinleistung ist die geometrische Sum-
me von Wirkleistung und Blindleistung.
Wenn: S = Scheinleistung
P = Wirkleistung
Q = Blindleistung
U
eff
= Spannung Effektivwert
I
eff
= Strom Effektivwert
ergibt sich für die Scheinleistung
S = P
2
+ Q
2
= U
eff
x J
eff
Leistungsfaktor
Der Leistungsfaktor PF (power factor) errechnet sich nach
der Formel:
PF = Leistungsfaktor
S = Scheinleistung
P = Wirkleistung
û = Spannung Spitzenwert
î = Strom Spitzenwert
Nur für sinusförmige Ströme und Spannungen
gilt: PF = cos ϕ
Ist zum Beispiel der Strom rechteckförmig und die Spannung
sinusförmig errechnet sich der Leistungsfaktor aus dem Ver-
hältnis von Wirkleistung zu Scheinleistung. Auch hier lässt
sich eine Blindleistung bestimmen. Aufgrund dessen, dass der
Strom eine andere Kurvenform besitzt als die Spannung, nennt
man diese Blindleistung auch Verzerrungsblindleistung.
û = 325,00 V; î = 12,25 A
û
U
eff
= —— = 229,8 V ≈ 230 V
√2
1 û · î
P =
——
∫ û · î sin ϕ · dϕ = ———
[
– cos ϕ
]
π
π
π
π
3
π
π
3
û · î 1,5
P =
———
[(
– (-1)
)
– (-0,5
)]
= —— · û · î
π π
1,5
=
—— · 325 V · 12,25 A = 1900 W
π
1
2π
I
eff
= ——
∫î
2
· dϕ
2π
0
2 2
= î
2
· —— = î · ——
3 3
2
I
eff
= 12,25 A · —— = 10,00 A
3
î
2
π 4π
=
—— ·
[(
π – ——
)
+
(
2π – ——
)]
2π 3 3
P 1900 W
PF = —— = —————— = 0,826
S 2300 VA
Q = S
2
– P
2
= (2300 VA)
2
– (1900 W)
2
= 1296 var

 Loading...
Loading...