Hameg HM8115-2 User Manual

9
Änderungen vorbehalten
3 Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
3.1 Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
3.2 Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Daraus ergibt sich die Formel für den sinusförmigen
Gleichrichtwert:
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= — ∫ Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= —
∫
Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
û
t
0
t
IuI
0
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= — ∫ Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
3.3 Effektivwert
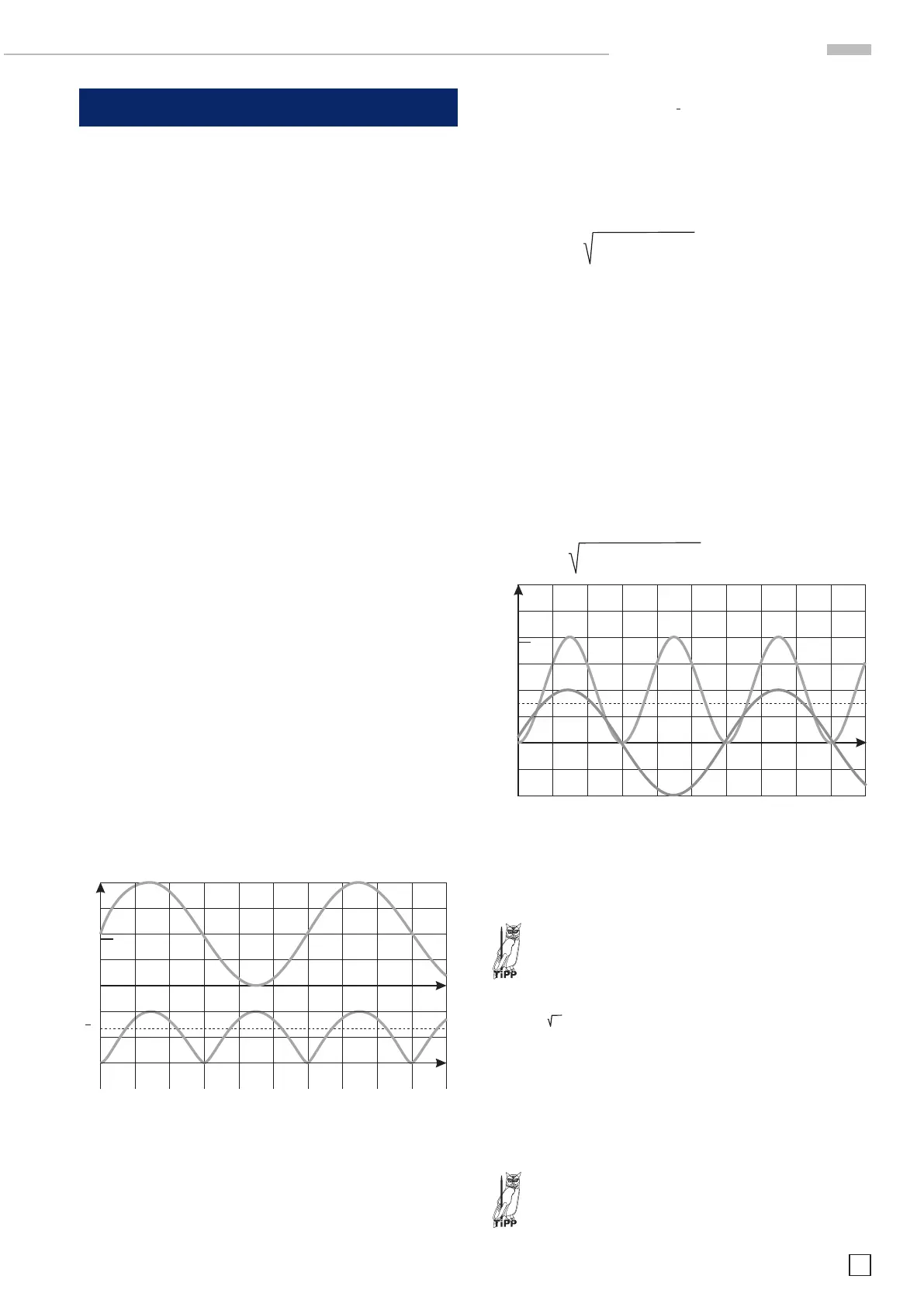
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechseln-
den Momentangrößen wird der Effektivwert (engl. RMS – Root
Mean Square) deniert. Der Effektivwert eines Wechsel-
signals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspannung
von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet genau-
so hell, wie eine Glühlampe versorgt mit einer Gleichspannung
von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
3.4 Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektivwert des Signals. Der Formfaktor eines Signals ermittelt
sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt der
Formfaktor:
3.5 Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude (Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= — ∫ Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= — ∫ Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
0
t
u (t)
2
u(t)
U
eff
9
Änderungen vorbehalten
Messgrundlagen
Verwendete Abkürzungen und Zeichen
W Wirkleistung P
VA Scheinleistung S
var Blindleistung Q
u(t) Spannung Momentanwert
u²(t) Spannung quadratischer Mittelwert
IÛI Spannung Gleichrichtwert
U
eff
Spannung Effektivwert
û Spannung Spitzenwert
I
eff
Strom Effektivwert
î Strom Spitzenwert
ϕ Phasenverschiebung (Phi) zwischen U und I
cos ϕ Leistungsfaktor bei sinusförmigen Größen
PF Leistungsfaktor (power factor) bei nichtsinusförmigen
Größen
Arithmetischer Mittelwert
Der arithmetische Mittelwert eines periodischen Signals ist
der gemittelte Wert aller Funktionswerte, die innerhalb einer
Periode T vorkommen. Der Mittelwert eines Signals entspricht
dem Gleichanteil.
– Ist der Mittelwert = 0 , liegt ein reines Wechselsignal vor.
– Für Gleichgrößen ist der Mittelwert = Augenblickswert.
– Für Mischsignale entspricht der Mittelwert dem Gleichan-
teil
Gleichrichtwert
Der Gleichrichtwert ist das arithmetische Mittel der Beträge
der Augenblickswerte. Die Beträge der Augenblickswerte er-
geben sich durch Gleichrichtung des Signals. Der Gleichricht-
wert wird berechnet durch das Integral über eine Periode von
Beträgen der Spannungs- oder Stromwerte.
Bei einer sinusförmigen Wechselspannung u(t) = û sin
ωt ist
der Gleichrichtwert das 2/π-fache (0,637fache) des Scheitel-
wertes. Hier Formel sinusförmiger Gleichrichtwert
Effektivwert
Der quadratische Mittelwert x²(t) eines Signals entspricht dem
Mittelwert des quadrierten Signals.
Wird aus dem quadratischen Mittelwert die Wurzel gezogen,
ergibt sich der Effektivwert des Signals X
eff
Bei Wechselspannungssignalen möchte man wie bei Gleich-
spannungssignalen die selben Formeln zur Berechnung von
Widerstand, Leistung, etc verwenden. Wegen der wechselnden
Momentangrößen wird der Effektivwert (engl. „RMS“ – Root
Mean Square) defi niert. Der Effektivwert eines Wechselsi-
gnals erzeugt den selben Effekt wie ein entsprechend großes
Gleichsignal.
Beispiel: Eine Glühlampe, versorgt mit einer Wechselspan-
nung von 230 V
eff
, nimmt die gleiche Leistung auf und leuchtet
genauso hell, wie eine Glühlampe versorgt mit einer Gleich-
spannung von 230 V
DC
.
Bei einer sinusförmigen Wechselspannung u(t) = û sin ωt ist
der Effektivwert das 1/√2-fache (0,707-fache) des Scheitel-
wertes.
Formfaktor
Wird der vom Messgerät ermittelte Gleichrichtwert mit dem
Formfaktor des Messsignals multipliziert ergibt sich der
Effektiv wert des Signals. Der Formfaktor eines Signals ermit-
telt sich nach folgender Formel:
Bei reinen sinusförmigen Wechselgrößen beträgt
der Formfaktor:
Crestfaktor
Der Crestfaktor (auch Scheitelfaktor genannt) beschreibt um
welchen Faktor die Amplitude ( Spitzenwert) eines Signals grö-
ßer ist als der Effektivwert. Er ist wichtig bei der Messung von
impulsförmigen Größen.
Bei reinen sinusförmigen Wechselgrößen beträgt
das Verhältnis: √2 = 1,414
û
t
0
t
IuI
0
0
t
u (t)
2
u(t)
U
eff
TiPP
Messgrundlagen
_
1
T
x
(t)
= — ∫ x
(t)
| · dt
T
0
I_
1
T
IxI
(t)
= — ∫ Ix
(t)
I · dt
T
0
I_
1
T
2
IuI = — ∫ Iû sin ωtI dt = — û = 0,637û
T
0
π
_
1
T
x
(t)
2
= — ∫ x
(t)
2
| · dt
T
0
1
T
x
eff
= — ∫ x
(t)
2
| · dt
T
0
1
T
û
U =
— ∫ (û sin ωt)
2
dt = — = 0,707û
T
0
2
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
TiPP
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
U
eff
Effektivwert
F = ——
= ——————————
IûI Gleichrichtwert
π
—— = 1,11
2 2
û
Spitzenwert
C = ——
= ——————————
U
eff
Effektivwert
Bezeichnung der Bedienelemente Messgrundlagen

Hameg HM8115-2 Specifications

General

Brand	Hameg
Model	HM8115-2
Category	Measuring Instruments
Language	English