Rebell SC2080 - Page 118

Podmenu Distr:
P ( [5][1]
Q ( [5][2]
R ( [5][2]
→ t [5][4]
Menu to można wykorzystać do obliczania prawdopodobieństwa standardowego
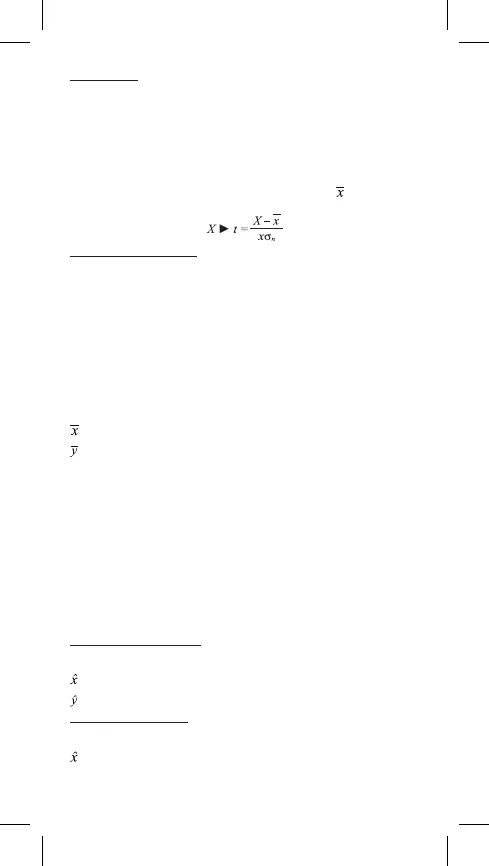
normalnego rozkładu. Normalizowana zmienna losowa t jest obliczana za po-
mocą wyrazu przedstawionego poniżej ze średnią wartością
i z wartością od-
chylenia xs
n
którą uzyskasz z danych wprowadzonych na ekranie STAT edytoru.
Statystyka dwóch zmiennych
Σx
[3](SUM)[2] Suma wszystkich wartości x lub y.
Σy
[3](SUM)[4]
Σx
2
[3](SUM)[1] Suma wszystkich wartości x
2
lub y
2
.
Σy
2
[3](SUM)[3]
Σx
3
[3](SUM)[6] Suma wszystkich wartości x
3
lub x
4
.
Σx
4
[3](SUM)[8]
Σxy
[3](SUM)[5] Suma parowych (x • y) zmiennych x-y.
Σx
2
y
[3](SUM)[7] Suma parowych (x
2
• y) zmiennych x-y.
n
[4](VAR)[1] Ilość włożonych wartości x-y.
[4](VAR)[2] Średnia wartości x lub y.
[4](VAR)[5]
xs
n-1
[4](VAR)[4] Wzorowe standardowe odchylenie wartości x lub y.
ys
n-1
[4](VAR)[7]
xs
n
[4](VAR)[3] Standardowe odchylenie wartości x lub y.
ys
n
[4](VAR)[6]
minX [6](MinMax)[1] Minimum wartości x.
maxX [6](MinMax)[2] Maksymum wartości x.
minY [6](MinMax)[3] Minimum wartości y.
maxY [6](MinMax)[4] Maksymum wartości y.
A [5](Reg)[1] Koecjent regresji A.
B [5](Reg)[2] Koecjent regresji B.
Dla regresji niekwadratowych:
r
[5](Reg)[3] Koecjent regresji r.
[5](Reg)[4] Oczekiwana wartość x.
[5](Reg)[5] Oczekiwana wartość y.
Dla regresji kwadratowych:
C [5](Reg)[3] Koecjent kwadratowy C z koecjentów regresji.
1
[5](Reg)[4] Oczekiwana wartość x1.
15–PL