Rebell SC2080 User Manual

Статистика одной переменной:
Σx
2
[3](SUM)[1] Сумма всех значений x
2
.
Σx
[3](SUM)[2] Сумма всех значений x.
n
[4](VAR)[1] Количество вложенных значений x.
[4](VAR)[2] Средняя величина значений x.
xs
n
[4](VAR)[3] Стандартное отклонение значений x.
xs
n–1
[4](VAR)[4] Эталонное стандартное отклонение значений x.
minX [6](MinMax)[1] Минимум значения x.
maxX [6](MinMax)[2] Максимум значения x.
Подменю Distr:
P ( [5][1]
Q ( [5][2]
R ( [5][2]
→ t [5][4]
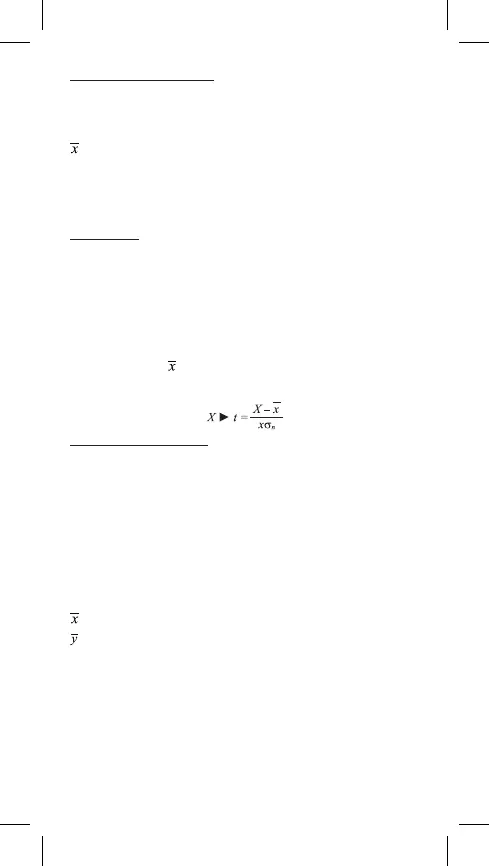
Настоящее меню можно использовать для вычисления вероятности
стандартного нормального разложения. Нормализованная случайная
переменная вычисляется при помощи выражения указанного ниже, со
средним значением
и с значением среднеквадратического отклонения
файла xs
n
которое получается из данных заданных на экране STAT
редактора.
Статистика двух переменных:
Σx
[3](SUM)[2] Сумма всех значений x или y.
Σy
[3](SUM)[4]
Σx
2
[3](SUM)[1] Сумма всех значений x
2
или y
2
Σy
2
[3](SUM)[3]
Σx
3
[3](SUM)[6] Сумма всех значений x
3
или x
4
.
Σx
4
[3](SUM)[8]
Σxy
[3](SUM)[5] Сумма парных (x • y) переменных x–y.
Σx
2
y
[3](SUM)[7] Сумма парных (x
2
• y) переменных x–y.
n
[4](VAR)[1] Количество вложенных значений x–y.
[4](VAR)[2] Средняя величина значений x или y.
[4](VAR)[5]
xs
n–1
[4](VAR)[4] Эталонное стандартное отклонение значений
x или y.
ys
n–1
[4](VAR)[7]
xs
n
[4](VAR)[3] Стандартное отклонение значений x или y.
ys
n
[4](VAR)[6]
minX [6](MinMax)[1] Минимум значения x.
maxX [6](MinMax)[2] Максимум значения x.
16–RU

Rebell SC2080 Specifications

General

Brand	Rebell
Model	SC2080
Category	Calculator
Language	English