16
G
RAPHING
T
ECHNOLOGY
G
UIDE
: TI-82
Copyright © Houghton Mifflin Company. All rights reserved.
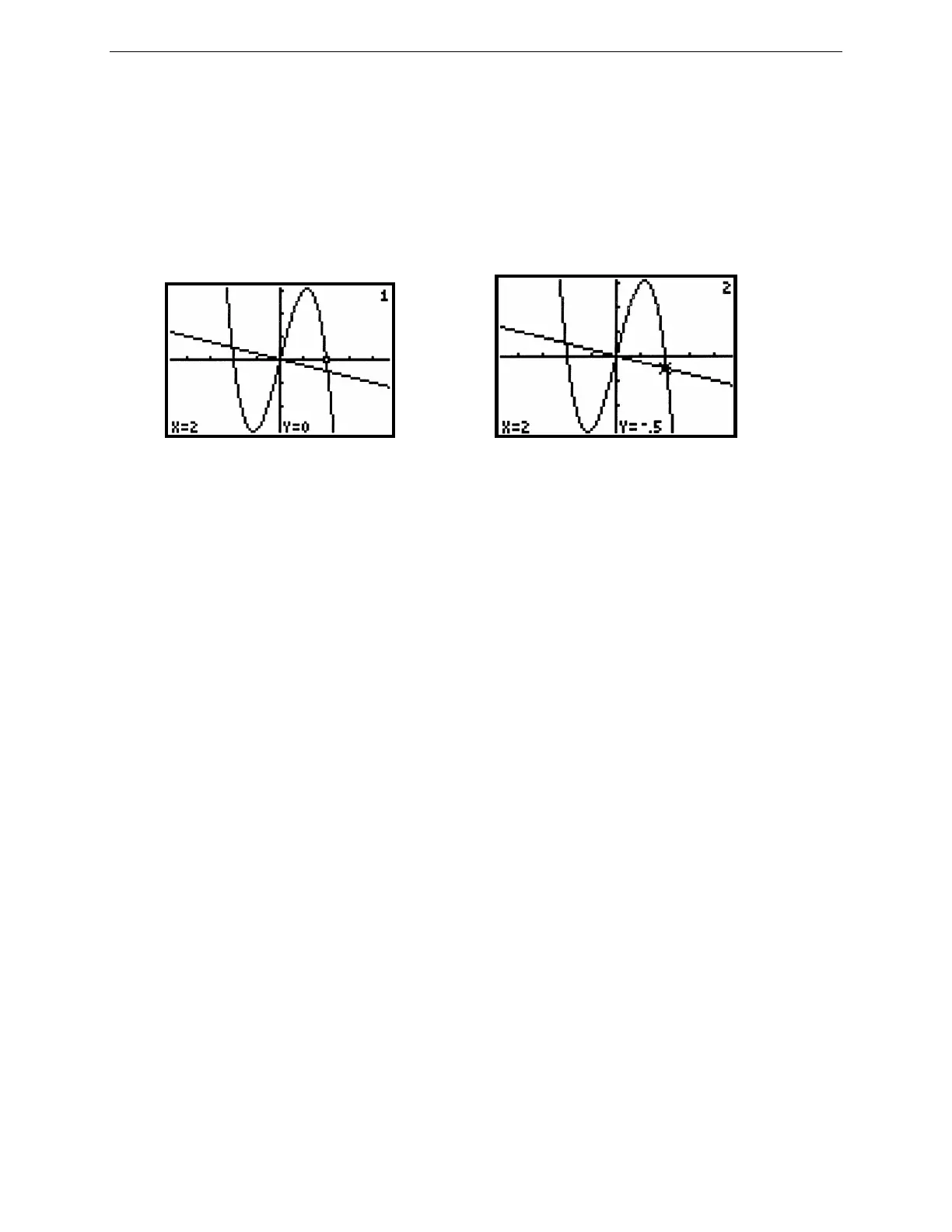
TRACE and ZOOM are especially important for locating the intersection points of two graphs, say the graphs of y =
–x
3
+ 4x and y = –.25x. Trace along one of the graphs until you arrive close to an intersection point. Then press ▲ or
▼ to jump to the other graph. Notice that the x-coordinate does not change, but the y-coordinate is likely to be
different (see Figures 2.47 and 2.48).
When the two y-coordinates are as close as they can get, you have come as close as you now can to the point of
intersection. So zoom in around the intersection point, then trace again until the two y-coordinates are as close as
possible. Continue this process until you have located the point of intersection with as much accuracy as necessary.
Figure 2.47: Trace on y = –x
3
+ 4x Figure 2.48: Trace on y = –.25x
You can also find the point of intersection of two graphs by pressing 2nd CALC 5. Trace with the cursor first along
one graph near the intersection and press ENTER; then trace with the cursor along the other graph and press
ENTER. Marks + are placed on the graphs at these points. Finally, move the cursor near the point of intersection
and press ENTER again. Coordinates of the intersection will be displayed at the bottom of the window.
2.3.2 Solving Equations by Graphing: Suppose you need to solve the equation 24x
3
– 36x + 17 = 0. First graph y =
24x
3
– 36x + 17 in a window large enough to exhibit all its x-intercepts, corresponding to all its roots. Then use trace
and zoom, or the TI-82’s root finder, to locate each one. In fact, this equation has just one solution, approximately x
= –1.414.
Remember that when an equation has more than one x-intercept, it may be necessary to change the viewing
rectangle a few times to locate all of them.
Technology Tip: To solve an equation like 24x
3
+ 17 = 36x, you may first transform it into standard form, 24x
3
–
36x + 17 = 0, and proceed as above. However, you may also graph the two functions y = 24x
3
+ 17 and y = 36x, then
zoom and trace to locate their point of intersection.
2.3.3 Solving Systems by Graphing: The solutions to a system of equations correspond to the points of intersection
of their graphs (Figure 2.49). For example, to solve the system y = x
2
– 3x – 4 and y = x
3
+ 3x
2
–2x – 1, first graph
them together. Then zoom and trace, or use the intersect option in the CALC menu, to locate their point of
intersection, approximately (–2.17, 7.25).
You must judge whether the two current y-coordinates are sufficiently close for x = –2.17 or whether you should
continue to zoom and trace to improve the approximation.
The solutions of the system of two equations y = x
3
+ 3x
2
– 2x –1 and y = x
2
– 3x – 4 correspond to the solutions of
the single equation x
3
+ 3x
2
– 2x –1 = x
2
– 3x – 4, which simplifies to x
3
+2x
2
+ x + 3 = 0. So you may also graph y =
x
3
+2x
2
+ x + 3 and find its x-intercepts to solve the system.

 Loading...
Loading...











