Torso Electronics T-1 - 3.2 Euclidean Sequencing Concept

51
The T-1 Notebook : Reference & Guide
50
The T-1 Notebook : Reference & Guide
Rhythmic Patterns
3
Rhythmic Patterns
3
NOTESNOTES
All tracks will play together in parallel controlled by a segment of the entire
pattern. One pattern will operate singularly while other patterns can be
queued or chained in series. The next pattern will play when the prior
completes. Patterns are by default 16 steps in length but can be extended
up to 64 steps or reduced. The quantize option is managed at pattern level.
Patterns will play and loop from the rst designated step (dened by rotation)
through to the last designated step (based on number of steps dened) and
then restart back to the rst step.
Each track can have an individual step count and settings which can help
create interesting polyrhythms and sequences.
Think in terms of a track being the ‘instrument’ mainly managed in the tonal
section. Think of a pattern as the ‘melody’. Rhythmic elements in the
pattern are mainly managed in the shape section. The quantize option is
only managed at pattern level.
Pulse View
1
1
1
1
1
9
4 5
12 13
8
16
8
413
16
16
Track 1
16 Steps
4 Pulses
7 Steps
3 Pulses
12 Steps
7 Pulses
Track 2 Track 3
7
12
9
512
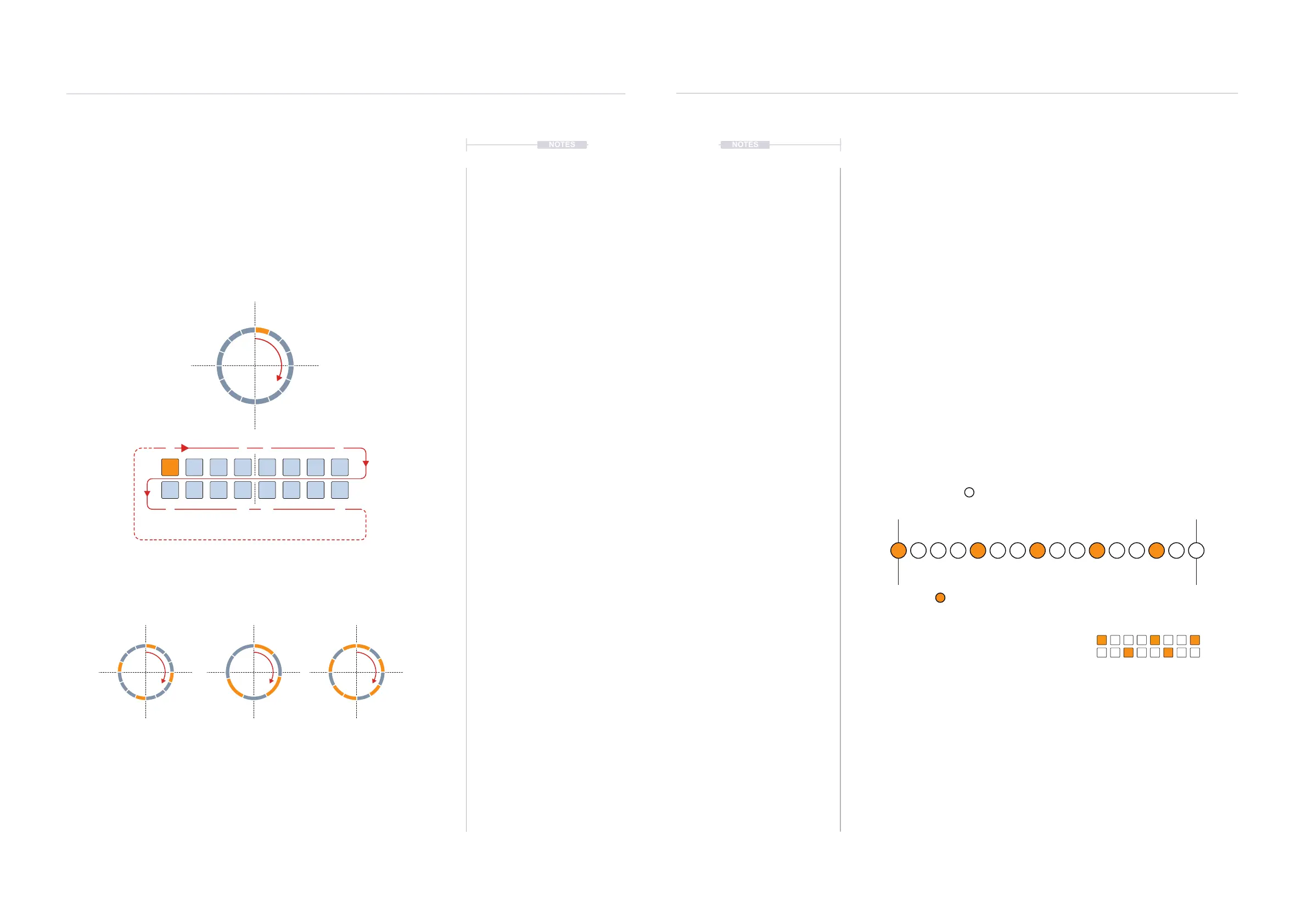
3.2 Euclidean Sequencing Concept
A sequence is a series of note events built within a pattern. T-1 uses a
number of generative models to develop a sequence. These models can be
combined to create elaborate and evolving patterns. Traditional note
placement is also possible. Two fundamental concepts used in T-1 are
Euclidean sequencing and Arpeggio’s. T-1’s parameters and setting build
on and around these models.
What is Euclidean Sequencing?
Euclidean geometry is a mathematical theory developed by Greek
mathematician Euclid. These formulas and applications have been
developed and evolved over time to become part of musical sequencing
algorithms.
At rst glance this may appear complex, but basic Euclidean sequencing is
actually quite simple. Essentially this model is based on the number of
steps in a pattern divided by the number of events. The events are then
spread as evenly as possible across the length of the pattern. Layering
patterns can then create interesting and intricate sequences.
Pattern = 16 Steps
16/5 = 3.2 Intervals. Population in reality is rounded.
Events = 5
1 16