9
Advanced Keyboard/CALCULUS USING THE SHARP EL-9900
Copyright © 2002, Sharp Electronics Corporation. Permission is granted to photocopy for educational use only.
9. Graph the second derivative by pressing Y= ENTER ENTER , and input
d/dx (Y2) in the Y3 location with the keystrokes MATH A (CALC)
0 5 (d/dx
() 2ndF VARS ENTER A (XY) 2 (Y2) and press )
ENTER .
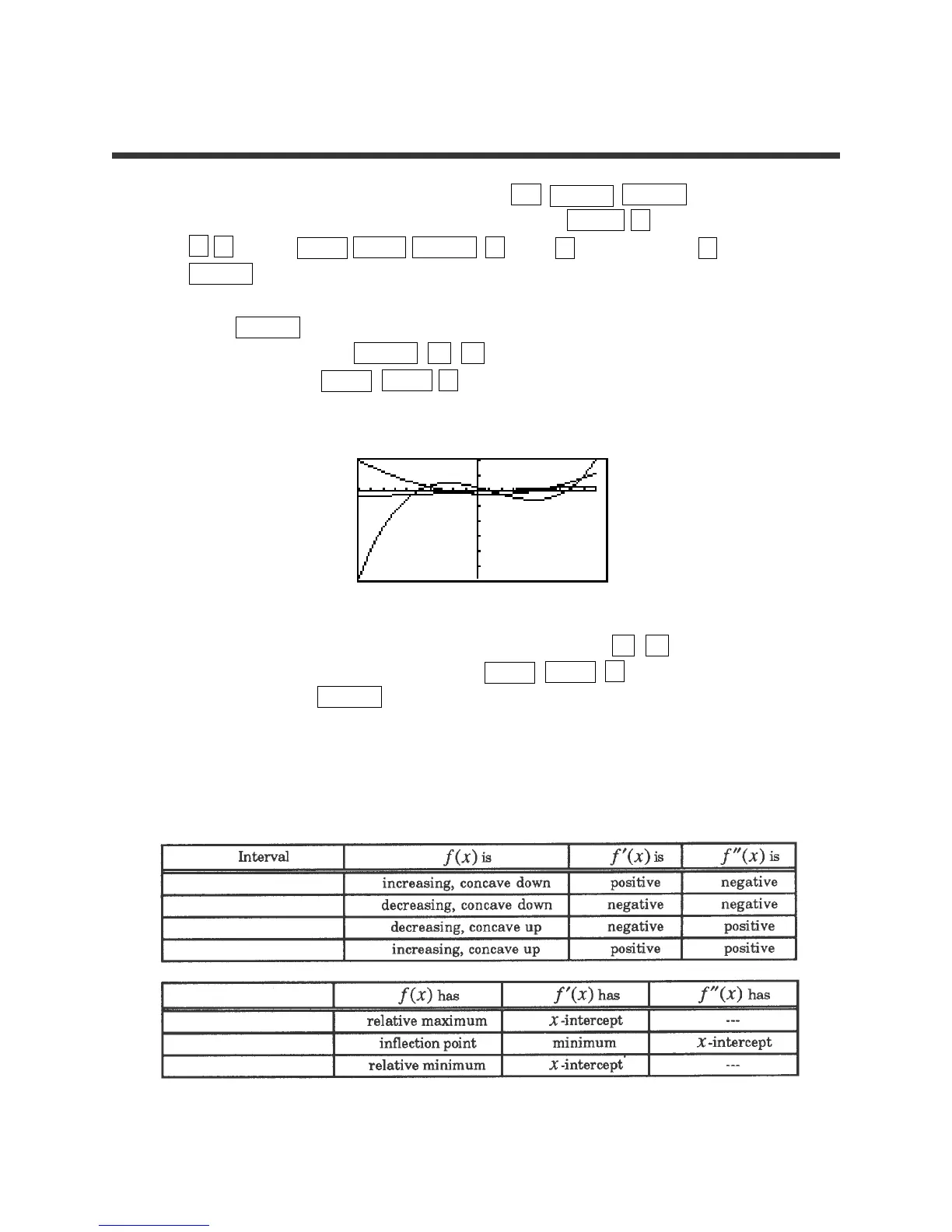
10. Press GRAPH to obtain the graphs of f(x), f ’(x), and f’’(x). Where is f’’(x).
zero? After pressing TRACE ▼▼to place the tracer on the second
derivative, press 2ndF CALC 5 (X_Incpt) to find that f’’(x) = 0 at
X= 1.167.
11. Find the y-value of this point of inflection by pressing ▲▲to move the
cursor to the original function. Press 2ndF CALC 1 (Value) and enter
1.167 and press ENTER .
12. The connections we have discovered between the graphs of f(x), f’(x), and
f’’(x) are summarized in the tables below.
GRAPHS OF DERIVATIVES (continued)
x <
-
2.4427
-
2.4427 < x < 1.1656
1.1656 < x < 4.776
x > 4.776
x – value
x =
-
2.4427
x = 1.16567
x = 4.776
To Next Page
Loading...
Need help?
General
