Texas Instruments TI-92+

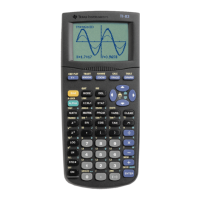
z
9
= a $ x
3
2$
y
3
2
+ b $ x
3
2
$ y
3
+ c $ x
3
$ y
3
2
+ d $ x
3
2
+ e $ y
3
2
+ f $ x
3
$ y
3
+ g $ x
3
+ h $ y
3
+ j
In matrix form this system is written as
[3]
x
1
2
$ y
1
2
x
1
2
$ y
1
x
1
$ y
1
2
x
1
2
y
1
2
x
1
y
1
x
1
y
1
1
x
1
2
$
y
2
2
x
1
2
$
y
2
x
1
$
y
2
2
x
1
2
y
2
2
x
1
y
2
x
1
y
2
1
x
1
2
$ y
3
2
x
1
2
$ y
3
x
1
$ y
3
2
x
1
2
y
3
2
x
1
y
3
x
1
y
3
1
x
2
2
$ y
1
2
x
2
2
$ y
1
x
2
$ y
1
2
x
2
2
y
1
2
x
2
y
1
x
2
y
1
1
x
2
2
$ y
2
2
x
2
2
$ y
2
x
2
$ y
2
2
x
2
2
y
2
2
x
2
y
2
x
2
y
2
1
x
2
2
$ y
3
2
x
2
2
$ y
3
x
2
$ y
3
2
x
2
2
y
3
2
x
2
y
3
x
2
y
3
1
x
3
2
$ y
1
2
x
3
2
$ y
1
x
3
$ y
1
2
x
3
2
y
1
2
x
3
y
1
x
3
y
1
1
x
3
2
$
y
2
2
x
3
2
$
y
2
x
3
$
y
2
2
x
3
2
y
2
2
x
3
y
2
x
3
y
2
1
x
3
2
$ y
3
2
x
3
2
$ y
3
x
3
$ y
3
2
x
3
2
y
3
2
x
3
y
3
x
3
y
3
1
$
a
b
c
d
e
f
g
h
i
=
z
1
z
2
z
3
z
4
z
5
z
6
z
7
z
8
z
9
or, in terms of equivalent matrix variables
[4]
X $ a = z
We could solve this system for the coefficients, but that requires inverting the X matrix. We can avoid
inverting the matrix, and get the solution more quickly, if we scale the x- and y-coordinates such that
[5]
x
1
h u
1
= 0x
2
h u
2
= 1x
3
h u
3
= 2
[6]
y
1
h v
1
= 0y
2
h u
2
= 2y
3
h v
3
= 2
We scale the original x and y variables (at which to interpolate) with
and [7]
u =





x−x
1
x
2
−x
1
x x < x
2
x−x
2
x
3
−x
2
+ 1
x
x
m
x
2





v =





y−y
1
y
2
−y
1
x y < y
2
y−y
2
y
3
−y
2
+ 1
x
y
m
y
2





With this scaling, the original 9x9 matrix becomes a matrix of constants, since all the u and v are
constants 0, 1 and 2, regardless of the actual values of x and y. Since the matrix is constant, its
inverse is constant, and we can calculate it once, in advance, and never need to calculate it again.
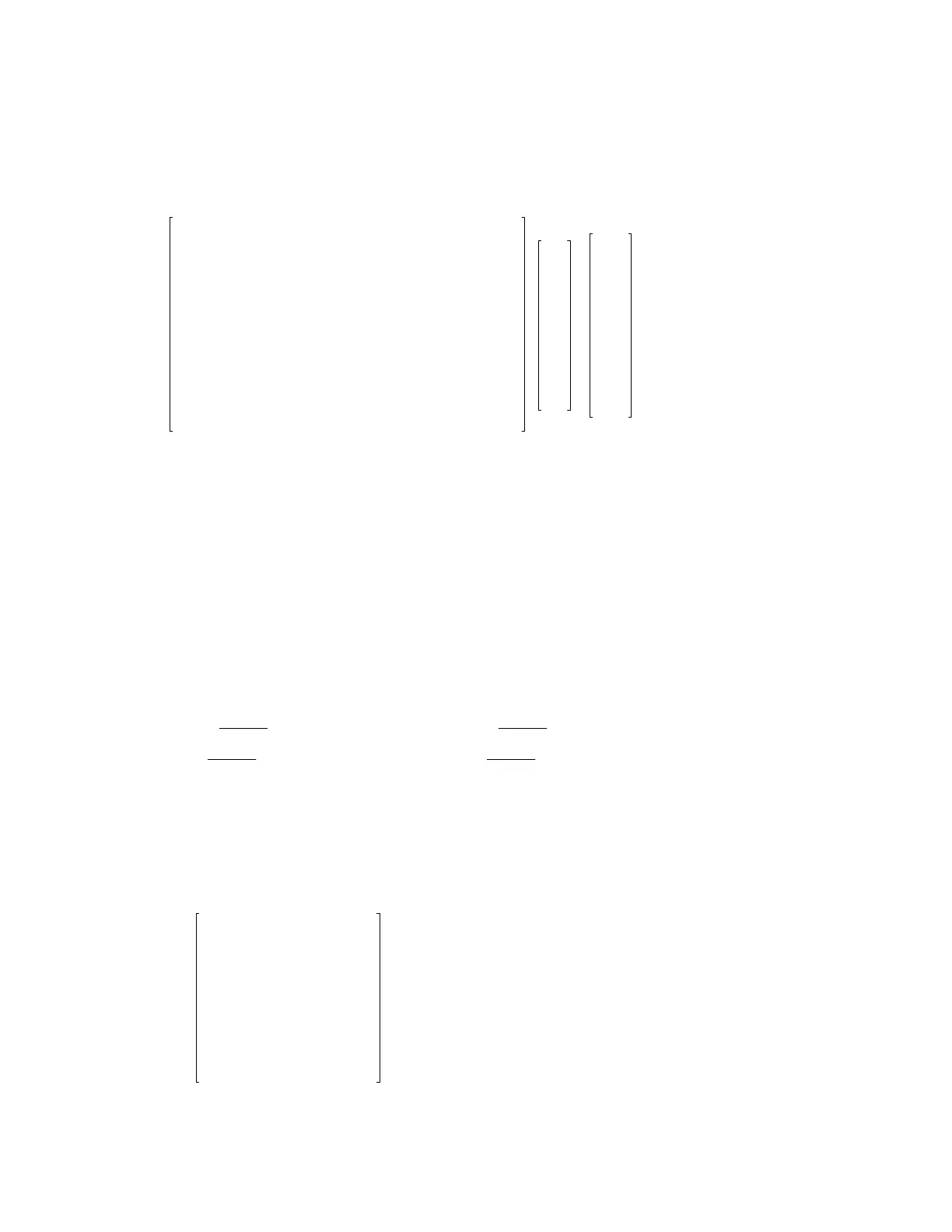
When we substitute the u's and v's for the x's and y's in the matrix, we have
[8]
X =
0 00000001
0 00010011
0 00040021
0 00100101
1 11111111
4 24142121
0 00400201
4 42412211
1688444221
6 - 49