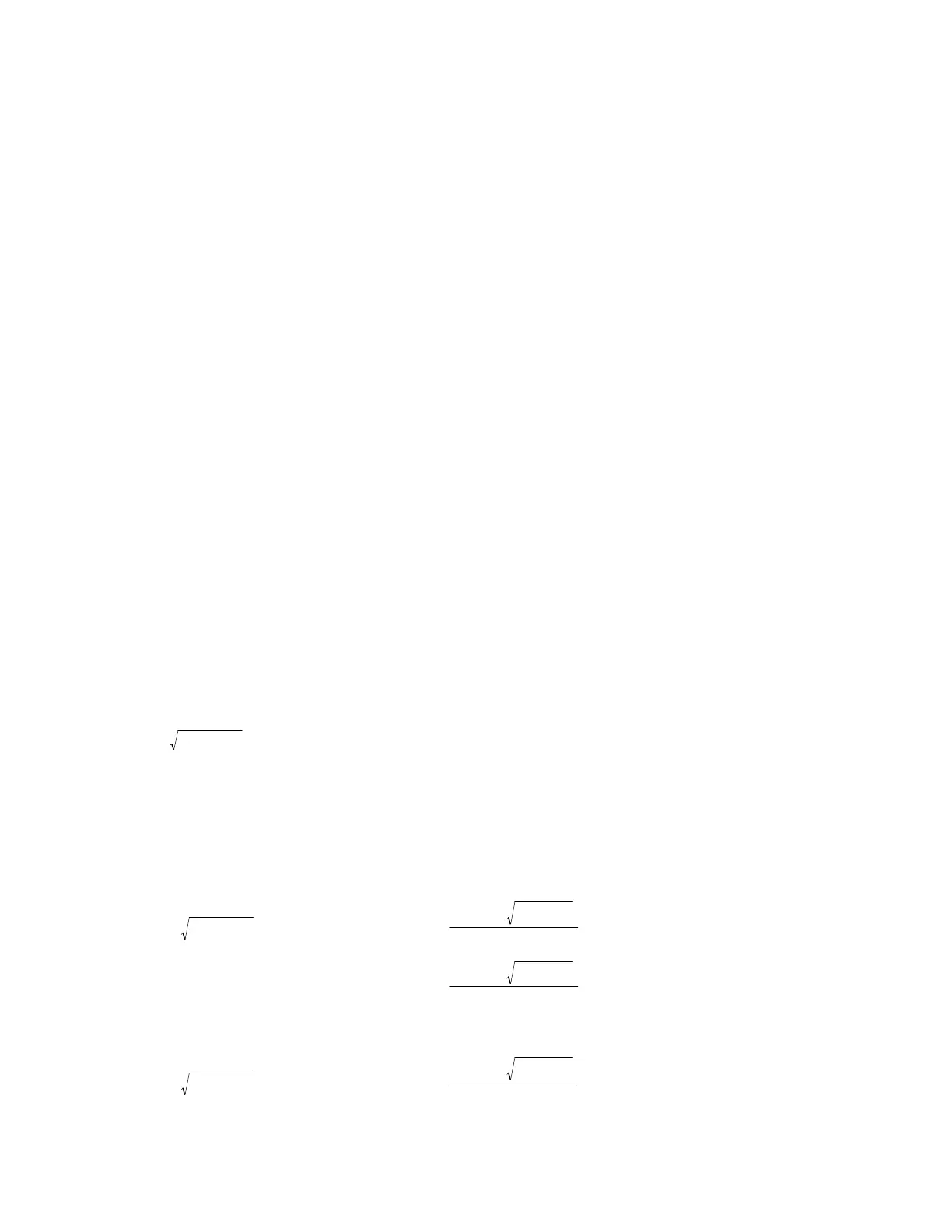rowdim(xx)→xxr
coldim(xx)→xxc
newmat(xxr,xxc)→r
for j,1,xxr
for k,1,xxc
f1(xx[j,k])→r[j,k]
endfor
endfor
return r
else
return "f1demo: type error"
endif
EndFunc
This function accepts arguments that may be expressions, numbers, lists or matrices. If the argument
is a list or matrix, the function is applied to each element. The function to be evaluated is defined as a
local function f1(); as an example, I use the ln() function. Your functions will probably be more
complicated.
The argument type is determined and saved in variable xxt. If the argument is a number, expression or
variable name, the argument is evaluated by the function and returned. If the argument is a list, the
seq() function is used to evaluate each list element, and return the results as a list. If the argument is a
matrix, two nested For ... EndFor loops are used to evaluate the function of each matrix element, and
the matrix is returned.
If the argument type is not supported, f1demo() returns the text string "f1demo: type error". The calling
program can test the type of the returned result and determine if an error occurred.
[6.41] Integration error in AMS 2.05
AMS 2.05 on TI89/92+ calculators can return incorrect results for indefinite and definite integrals which
include, in the integrand, the expression
(
ax + b
)
n
where x is the integration variable and a, b and n are constants. This bug has been reported by
Damien Cassou and others.
One solution is to use the exponential form for the integrand, instead of the square root operator.
For example, in Auto mode,
returns [1]
¶
(
7x + 4
)
3
dx
2
(
7x+4
)(
7x+4
)
3
5
while the correct result should be
2
(
7x+4
)(
7x+4
)
3
35
Another example of an incorrect result is
which returns [2]
¶
(
2x − 3
)
7
dx
2
(
2x−3
)(
2x−3
)
7
7
6 - 73
To Next Page
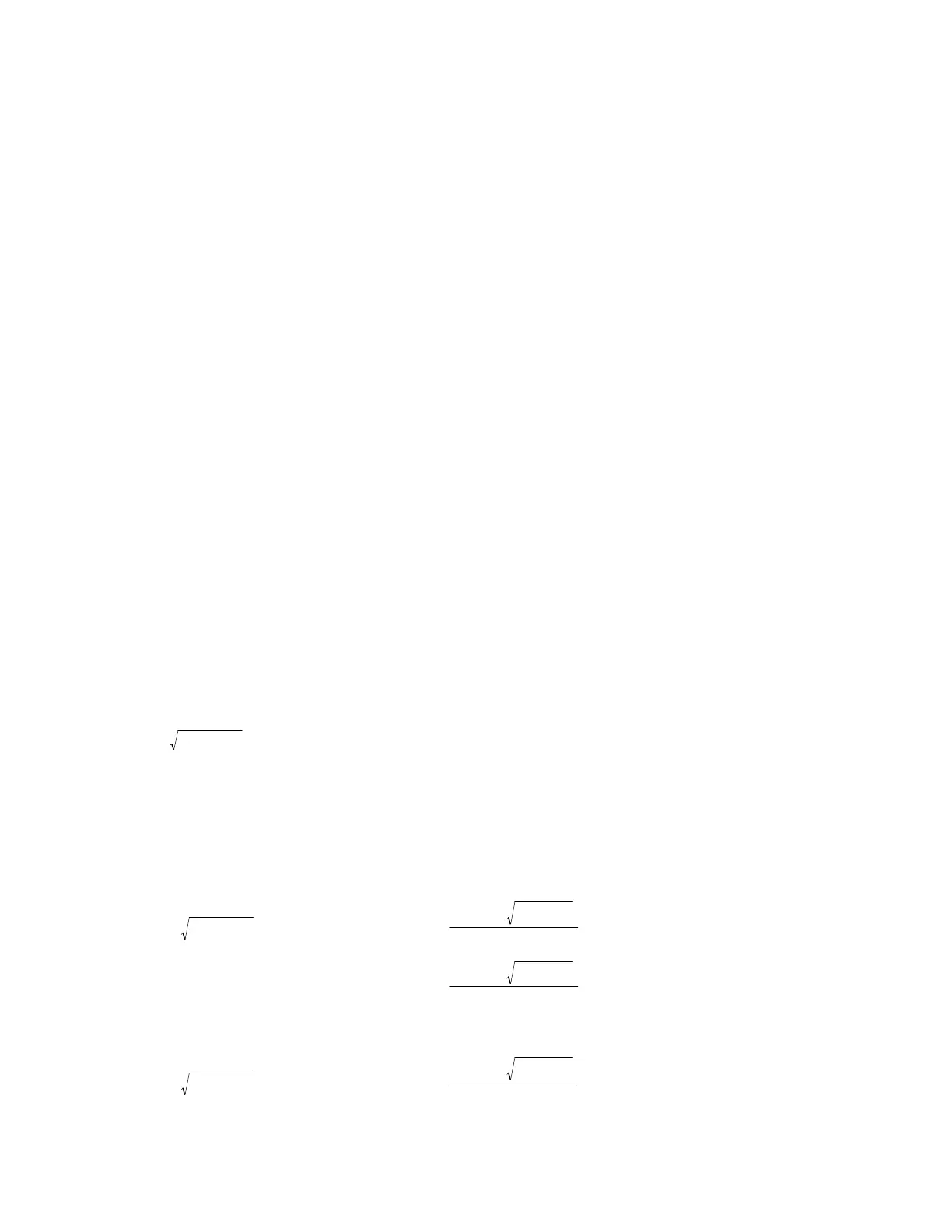Loading...
Need help?
General
