53
History and Theory of Infrared Technology
According to Kirchho’s law, for any
material the spectral emissivity and
spectral absorptance of a body are
equal at any specied temperature and
wavelength. That is:
ε
λ
= α
λ
From this we obtain, for an opaque
material (since α
λ
+ ρ
λ
= 1):
ε
λ
+ ρ
λ
= 1
For highly polished materials ε
λ
approaches zero, so for a perfectly
reecting material (for example. a perfect
mirror) we have:
ρ
λ
= 1
For a graybody radiator, the Stefan-
Boltzmann formula becomes:
W = εσT
4
[Watt/m
]
This states that the total emissive power
of a graybody is the same as a blackbody
at the same temperature reduced in
proportion to the value of ε from the
graybody.
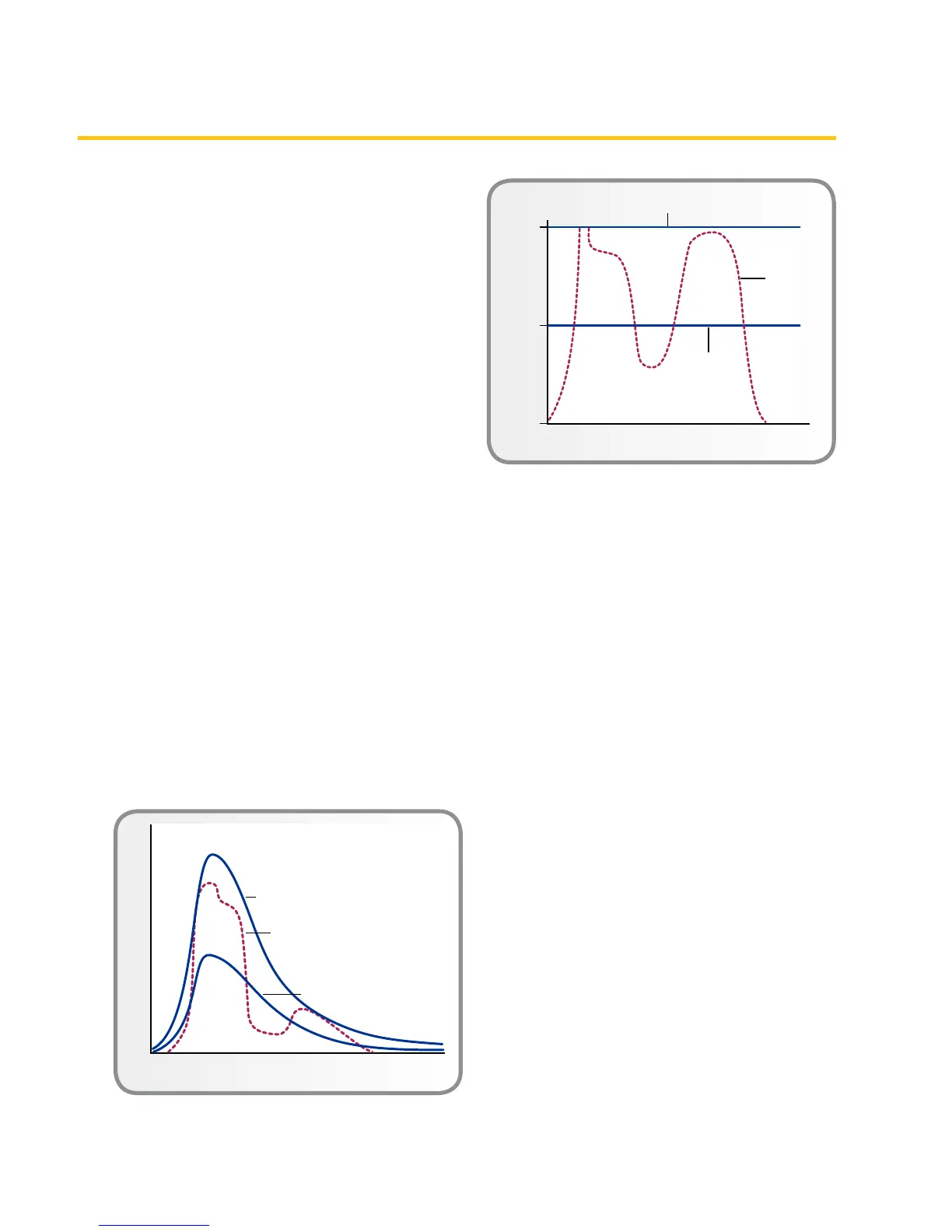
Figure 13. Spectral emissivity of three types of
radiators.
Infrared Semi-transparent Materials
Consider a non-metallic, semi-
transparent body in the form of a thick
at plate of plastic material. When the
plate is heated, radiation generated
within its volume must work its way
toward the surfaces through the
material in which it is partially absorbed.
Moreover, when it arrives at the surface,
some of it is reected back into the
interior. The back-reected radiation is
again partially absorbed, but some of
it arrives at the other surface, through
which most of it escapes, but part of it
is reected back again. Although the
progressive reections become weaker
and weaker, they must all be added up
when the total emittance of the plate is
sought. When the resulting geometrical
series is summed, the eective emissivity
of a semi-transparent plate is obtained as:
(1 –ρ
λ
) (1 – τ
λ
)
ε
λ
=
______________
1 – p
λ
t
λ
When the plate becomes opaque this
formula is reduced to the single formula:
ε
λ
= 1 – p
λ
To Next Page
Loading...
Need help?
General
