HP HP-15C Advanced Functions Handbook

Section 1: Using | SOLVE] Effectively 9
I SOLVE | abandons the search for a root only when three successive
parabolic fits yield no decrease in the function magnitude or when
d — b. Under these conditions, the calculator displays Error 8.
Because b represents the point with the smallest sampled function
magnitude, b and f(b) are returned in the X- and Z-registers,
respectively. The Y-register contains the value of a or c. With this
information, you can decide what to do next. You might resume the
search where it left off, or direct the search elsewhere, or decide
that f(b) is negligible so that x = b is a root, or transform the
equation into another equation easier to solve, or conclude that no
root exists.
Handling Troublesome Situations
The following information is useful for working with problems that
could yield misleading results. Inaccurate roots are caused by
calculated function values that differ from the intended function
values. You can frequently avoid trouble by knowing how to
diagnose inaccuracy and reduce it.
Easy Versus Hard Equations
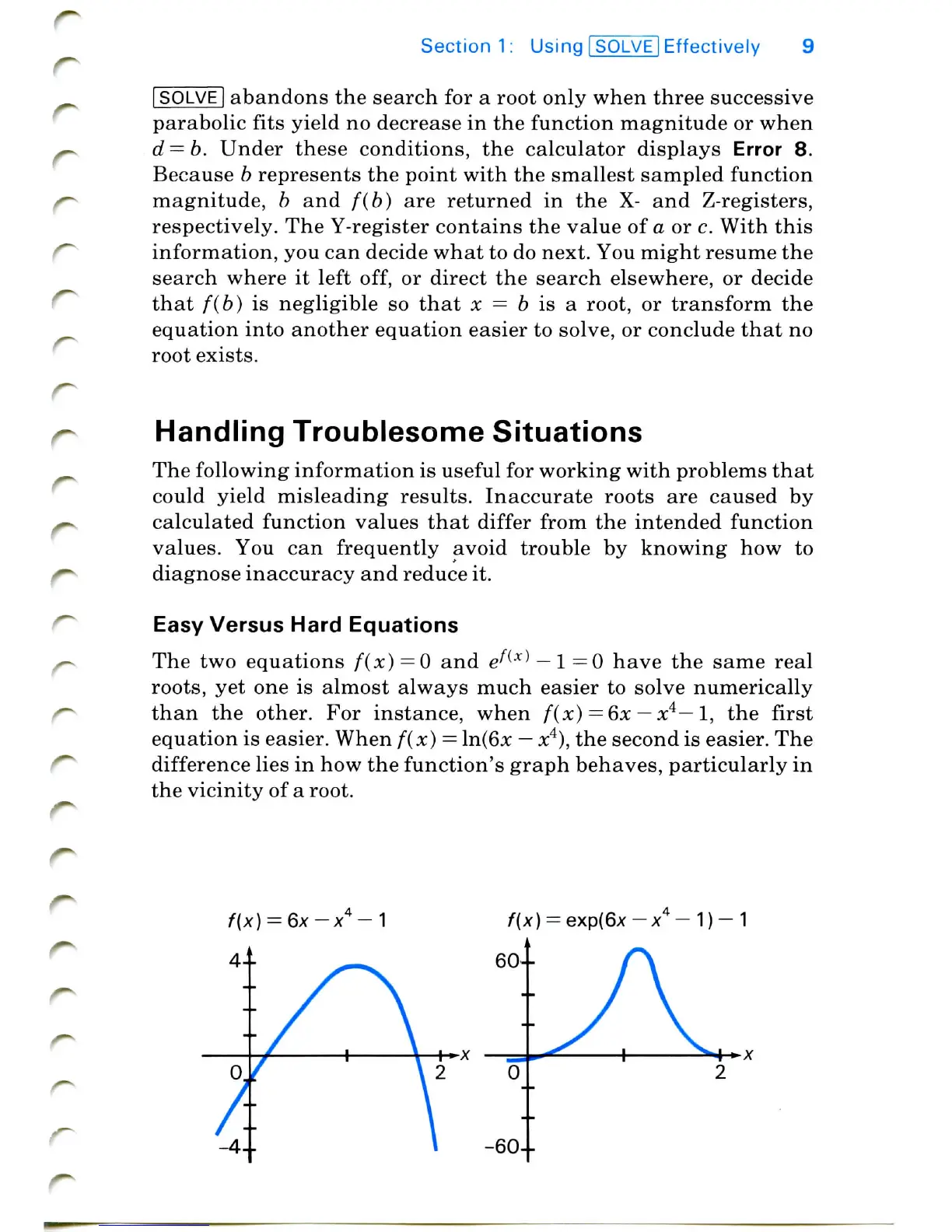
The two equations f(x) = 0 and e^(x) — 1=0 have the same real
roots, yet one is almost always much easier to solve numerically
than the other. For instance, when f(x) = 6x — x4— 1, the first
equation is easier. When f(x) = ln(6x — x4), the second is easier. The
difference lies in how the function's graph behaves, particularly in
the vicinity of a root.
/(x) = 6x-x -1
4-- 60--
-60--

HP HP-15C Specifications

General

Brand	HP
Model	HP-15C
Category	Calculator
Language	English