HP HP-15C - Page 114

112 Section 4: Using Matrix Operations
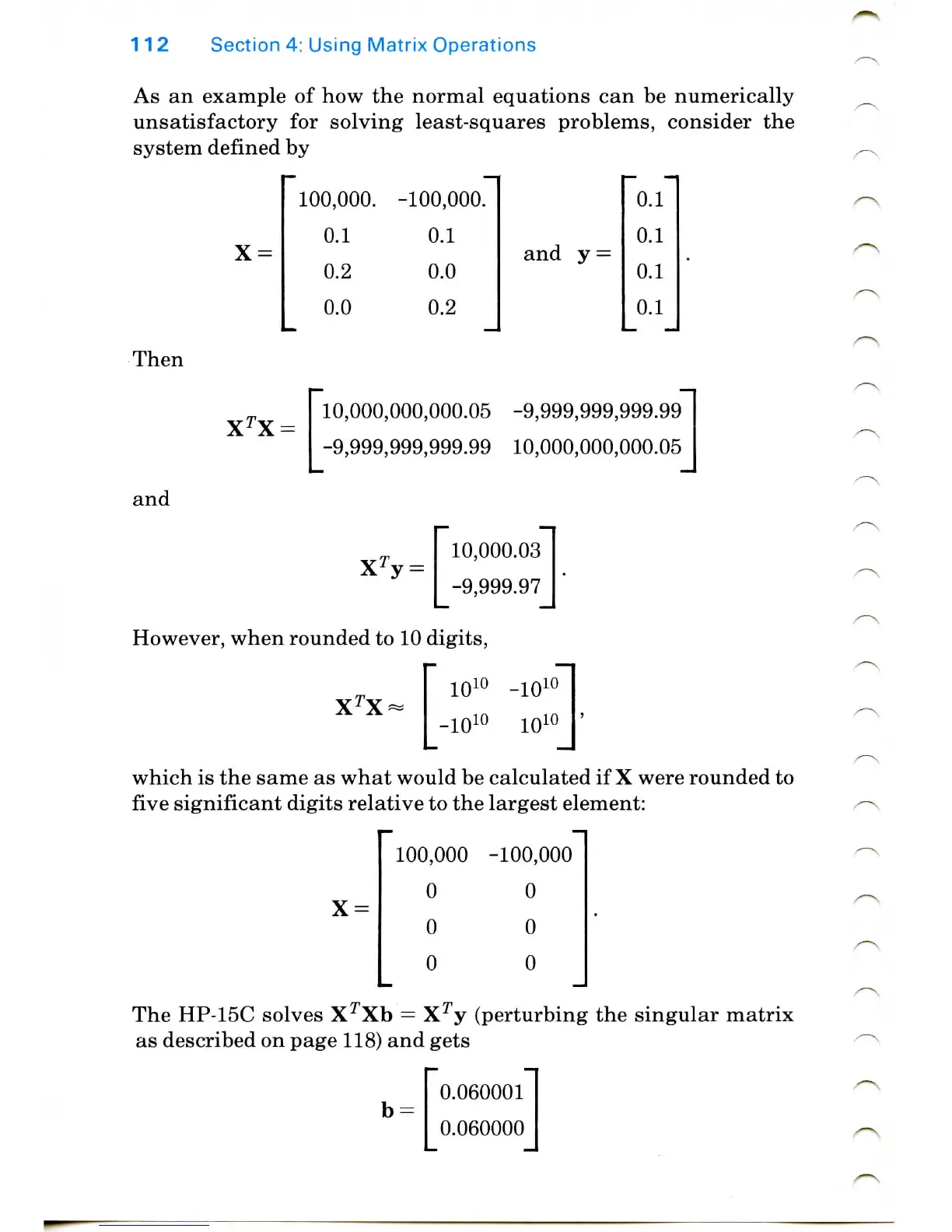
As an example of how the normal equations can be numerically
unsatisfactory for solving least-squares problems, consider the
system defined by
X =
100,000. -100,000.
0.1 0.1
0.2 0.0
0.0 0.2
and y =
0.1
0.1
0.1
0.1
Then
and
10,000,000,000.05 -9,999,999,999.99
-9,999,999,999.99 10,000,000,000.05
10,000.03
-9,999.97
However, when rounded to 10 digits,
1010 -1010
-1010 1010
which is the same as what would be calculated if X were rounded to
five significant digits relative to the largest element:
100,000 -100,000
0 0
0 0
0 0
The HP-15C solves XTXb = XTy (perturbing the singular matrix
as described on page 118) and gets
0.060001
0.060000