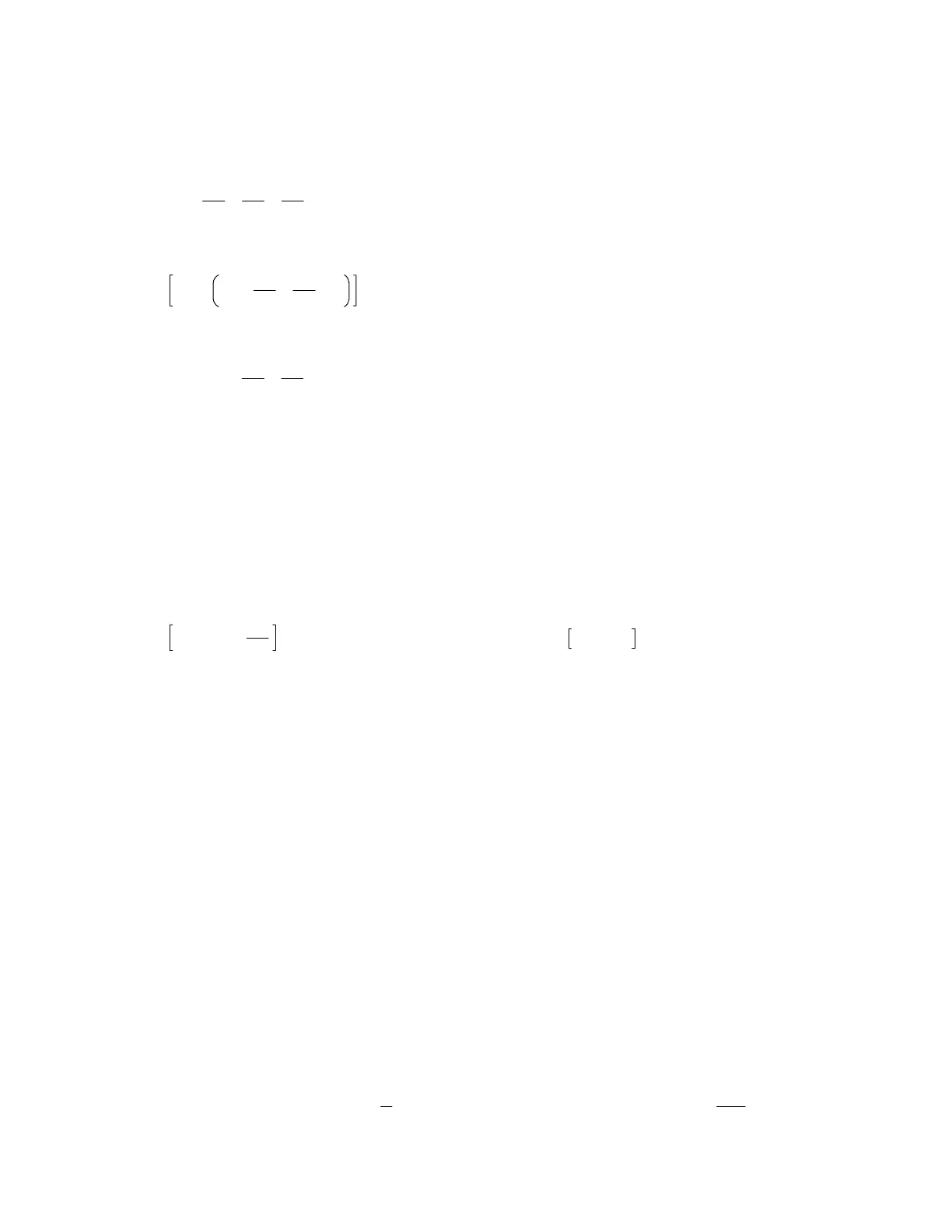The function starts getting erratic at about 370, and really gets chaotic at about x = 530. Since the limit
of f(x) is one, there are definite problems in evaluating the function. As the problem occurs for large x,
an asymptotic expansion is a potential solution. An asymptotic expansion is a series of the form
[2]
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+ ...
which is defined for sufficiently large x, if, for every n = 0, 1, 2, 3, ...
as [3]
f
(
x
)
−
a
0
+
a
1
x
+
a
2
x
2
+ ...
x
n
d
0x
d∞
then
[4]
f
(
x
)
l a
0
+
a
1
x
+
a
2
x
2
+ ...
Note that [2] may not converge for any x. In general, finding an asymptotic expansion is difficult, and
many books have been written about the difficulties and some solutions. However, since we are only
interested in a numeric approximation, our task is a little easier. Since [3] is defined for every value of n
= 1, 2, 3, ..., we find a
0
by letting n = 0, then [3] becomes
or
f
(
x
)
− a
0
d
0a
0
= lim
x
d∞
f
(
x
)
To find the second term a
1
, we have
or
f
(
x
)
− a
0
−
a
1
x
x
d
0a1= lim
x
d∞
f
(
x
)
− a
0
x
We can find as many terms as necessary by repeating this process, which is automated by this
function asympexp():
asympexp(fx,x,n)
Func
©(f(x),x,number of terms) Asymptotic expansion
©returns {an,...,a0}
©4jun02/dburkett@infinet.com
local i,j,a
{}→a
limit(fx,x,∞)→a[1]
for i,1,n-1
limit(x^i*(fx-Σ(a[j+1]/x^j,j,0,i-1)),x,∞)→a[i+1]
endfor
seq(a[i],i,dim(a),1,⁻1)
EndFunc
asympexp() should be run in Exact mode, since it used the Limit() function. asympexp() runs very
slowly, but eventually returns these terms:
a
0
= 1
a
1
=−
3
5
a
2
= 0a
3
=−
4
175
6 - 128
To Next Page
Loading...
Need help?
General
