5 - 10
● Floating Point Number:
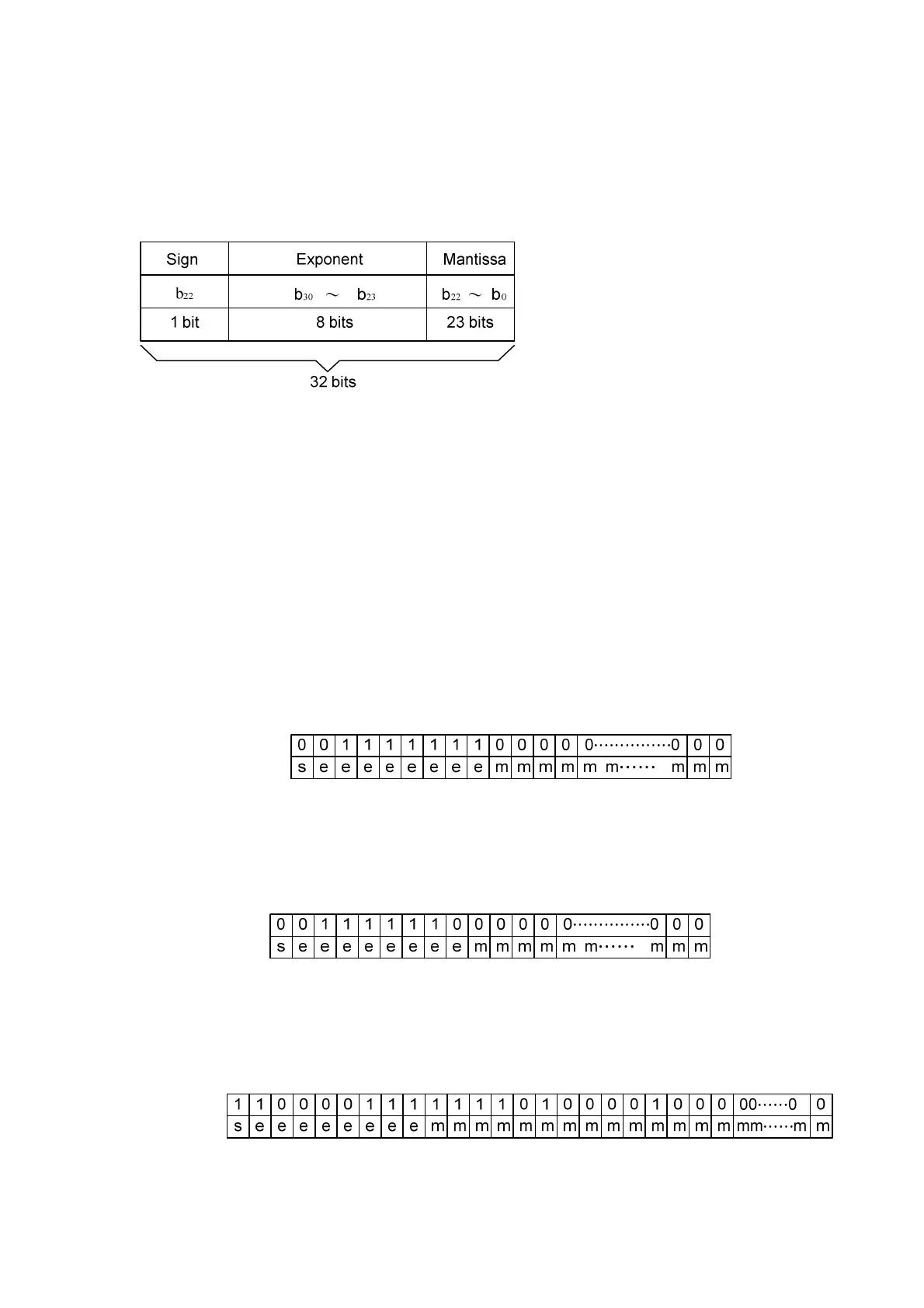
The format of floating point number of Fatek-PLC follows the IEEE-754 standard, which use a double word for storage
and can be expressed as follow:
floating point number = sign + Exponent + Mantissa
▲ If the sign bit is 0 the number is positive, if the sign bit is 1 the number is negative.
▲ The exponent is denoted as 8-bit excess 127.
▲ The mantissa is 23-bit with radix 2. A normalized mantissa always starts with a bit 1, followed by
the radix point, followed by the rest of the mantissa. The leading bit 1, which is always present in a
normalized mantissa, is implicit and is not represented.
● The Conversion rule of Integer to floating is :
N = ( -1)
S
* 2
(E -127)
* ( 1.M ) 0 < E < 255
For example :
(1). 1 = ( -1 )
0
* 2
( 01111111 )
* ( 1.000………0 )
The sign is represented by 0, the exponent's code in excess 127 is 127 = 01111111, and the significant
bit is 1, resulting in the mantissa being all O's. The simple precision IEEE 754 representation of 1, is
thus :
= 3F800000H
(2). 0.5 = ( -1 )
0
* 2
( 01111110 )
* ( 1.000………0 )
The sign is represented by 0, the exponent's code in excess 127 is 127 - 1 = 01111110, and the
significant bit is 1, resulting in the mantissa being all O's. The simple precision IEEE 754 representation
of 0.5, is thus :
= 3F000000H
(3). -500.125 = ( -1 )
1
* 2
( 10000111 )
* ( 1. 11110100001000000000000)
The sign is represented by 0, the exponent's code in excess 127 is 127 - 1 = 01111110, and the
significant bit is 1, resulting in the mantissa being all O's. The simple precision IEEE 754 representation
of -500.125, is thus :
= C3FA1000H
Code( 1 ) =
Code( 0.5 ) =
Code( -500.125 ) =
 Loading...
Loading...