Appendix D: A Detailed Look at _ 227
Special consideration is required for a different
type of situation in which _ finds a root
with a nonzero function value. If your
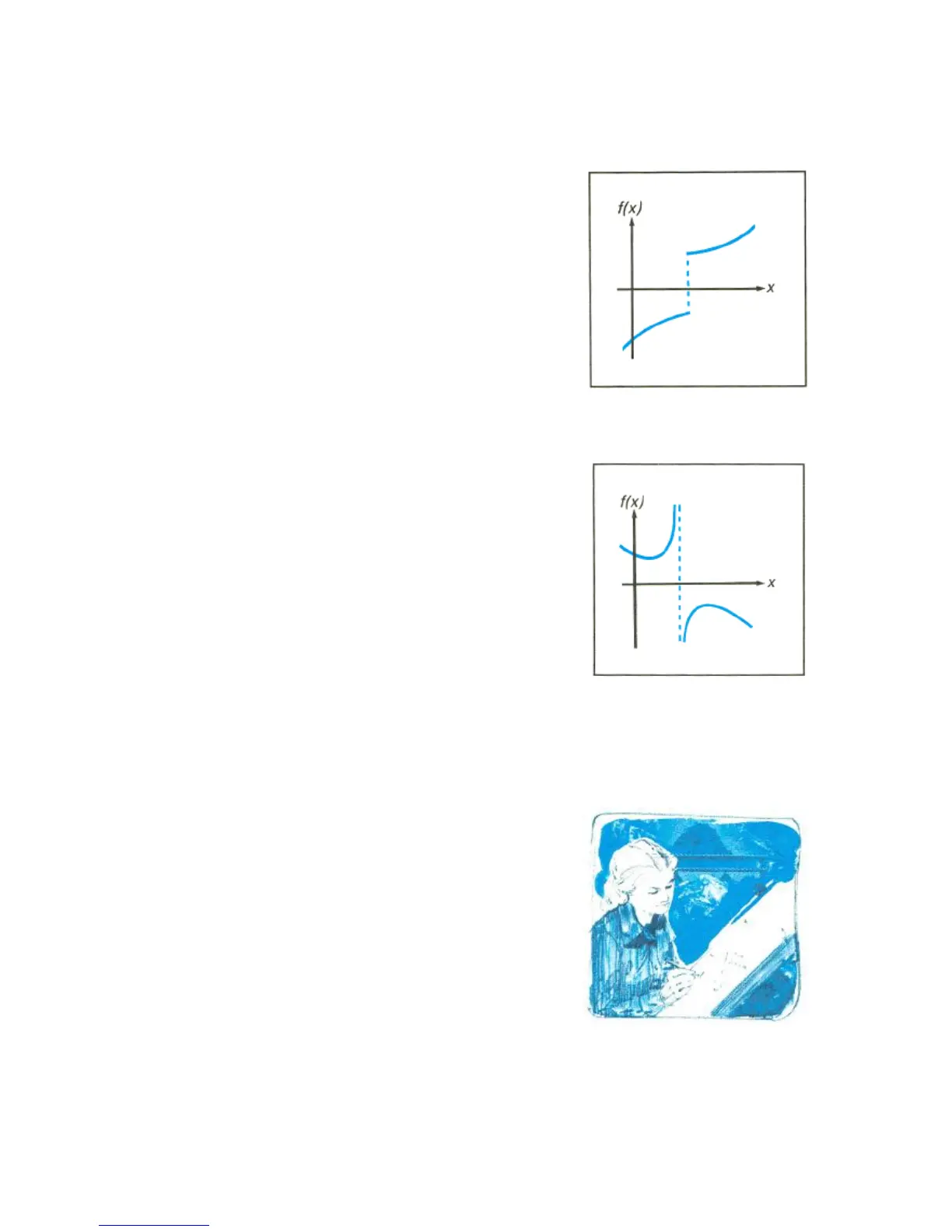
function's graph has a discontinuity that
crosses the x-axis, _ specifies as a root
an x-value adjacent to the discontinuity. This is
reasonable because a large change in the
function value between two adjacent values of
x might be the result of a very rapid,
continuous transition. Because this cannot be
resolved by the algorithm, the root is displayed
for you to interpret.
A function may have a pole, where its
magnitude approaches infinity. If the function
value changes sign at a pole, the corresponding
value of x looks like a possible root of your
equation, just as it would for any other
discontinuity crossing the x-axis. However, for
such functions, the function value placed into
the Z-register when that root is found will be
relatively large. If the pole occurs at a value of
x that is exactly represented with 10 digits, the
subroutine may try that value and halt prematurely with an error indication.
In this case, the _ operation will not be completed. Of course, this
may be avoided by the prudent use of a conditional statement in your
subroutine.
Example: In her analysis of the stresses in a
structural component, design consultant Lucy
I. Beame has determined that the shear stress
can be expressed as

 Loading...
Loading...