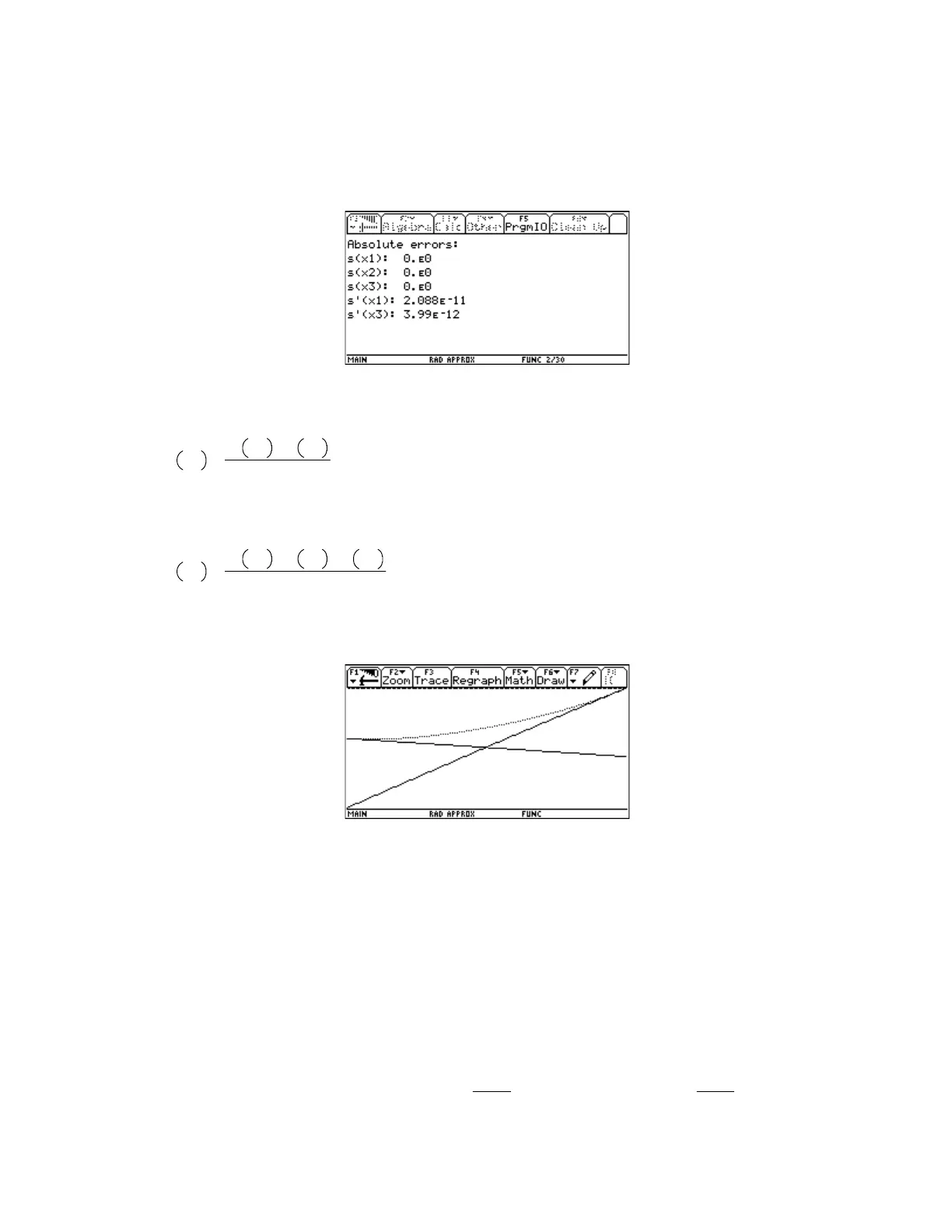
For f1(x) and f2(x), I can just enter y1(x) and y2(x), since I have previously defined these functions in
the Y= Editor. I set the splice center and half-width, and chose 'center' for the s(x2) method. I need not
enter a value for 'manual s(x2)', since I am not using the manual method. After pressing [ENTER], the
errors are shown on the program I/O screen:
spli4ui() supports three options to set s(x2): center, mean and manual. With the 'manual' s(x2) method,
you specify s(x2) in the 'manual s(x2)' field. The 'center' method sets
s x
2
=
f
1
x
1
+f
2
x
2
2
so use the 'center' method to force the splice midway between two functions which do not intersect, or
to force the splice through f
1
(x
2
) = f
2
(x
2
). The 'mean' method sets
s x
2
=
f
1
x
1
+f
1
x
2
+f
2
x
3
3
so use this method to force the splice through a point away from both functions. For example, this plot
shows the splice and function differences with the mean method:
Scaling the derivatives
Since the x- and y-data are scaled to avoid a singular matrix, we must also scale the derivatives of f
1
(x)
and f
2
(x) to be consistent with the scaled x values. Starting with a general function
y = f
(
x
)
and the general scaling equations
x
s
= p
$
x + qy
s
= r
$
y + s
we solve for x and y,
x =
x
s
−q
p
y =
y
s
−s
r
6 - 108
 Loading...
Loading...











