ALESIS FUSION
ANALOG SYNTHESIS TUTORIAL
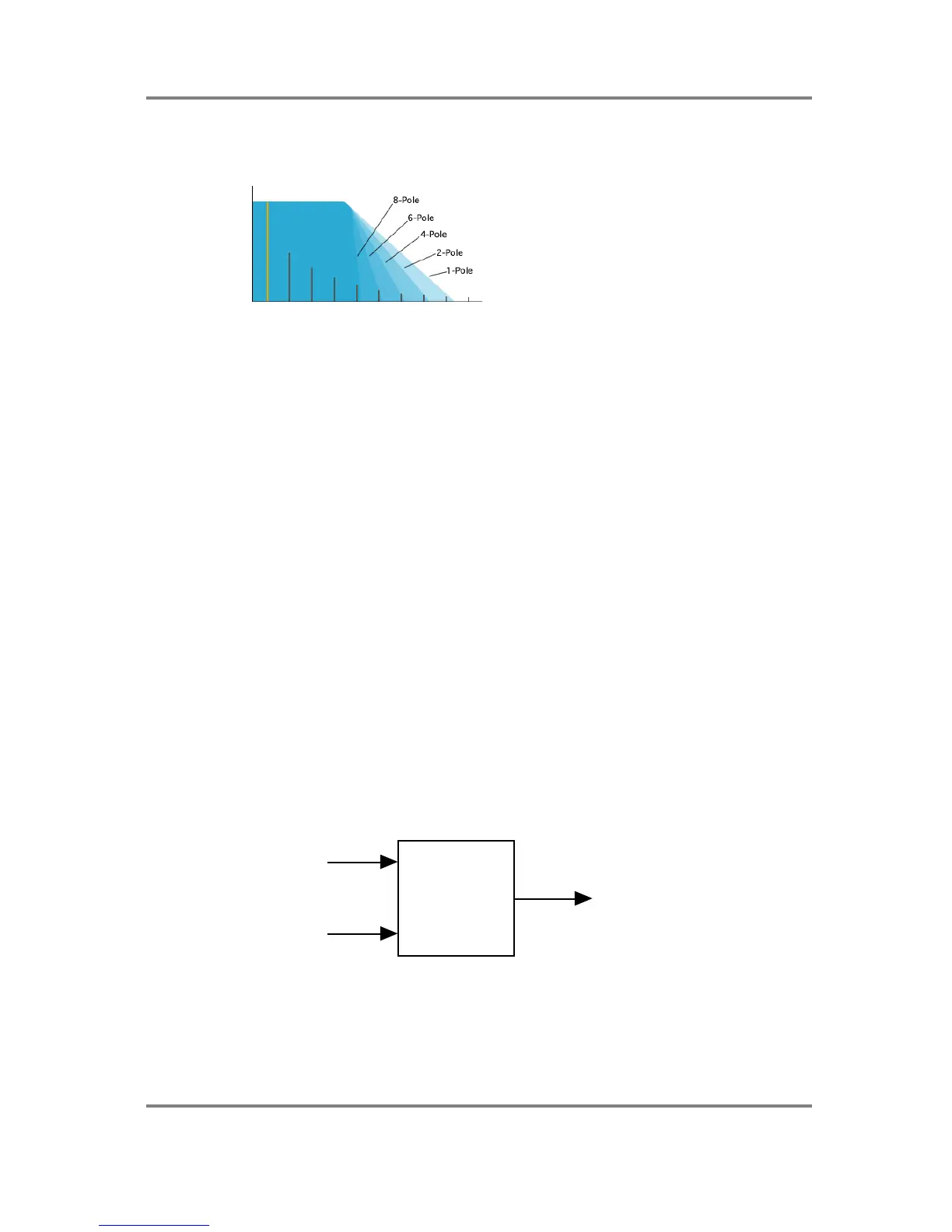
Recent advances in DSP technology means that almost any roll-off can be
defined and we can
have anything from 1-pole (6dB/Octave) to 8-pole (48dB/Octave):
And if you are wondering what the dB/Octave refers to..... it’s the
amount of attenuation of
level per octave.
Thus a 6dB/Octave filter cuts 6dBs (decibels) for every octave and a
24dB/Octave filter cuts 24dBs for every octave and therefore has a more dramatic (some
would
say ‘punchy’) effect on the sound. You can largely forget the technicalities though - the rule of
thumb is that a 1-pole (6dB/Octave) filter is going to have a mild effect
on the sound whereas a
4-pole (24dB/Octave) or higher filter is going to have a more dramatic effect. In
practice, 2-pole
and 4-pole filters are the most commonly used as they are arguably the most ‘musical’.
Filters - Conclusion
To regard the
filters as static tone controls is only half the story - they come to life when their
cutoff
frequency changes over time. This can be done in several ways but almost always
involves using a controller of some sort such as an envelope generator,
LFO or real-time
controller (such as a mod wheel).
Almost all sounds
vary in tone/timbre over time and the filter is the ideal tool to mimic that
phenomenon. Even if your intention is not to replicate acoustic
sounds, synth sounds can be
significantly improved if they also have harmonic movement and change during the
course of a
note - for example, a resonant synth bass sound can benefit greatly from having cutoff
frequency controlled by a decaying envelope as well as having the
cutoff frequency controlled
by velocity so that the sound is brighter when played hard and
vice versa
.
We will come to this soon when we look at envelope generators and later when we
examine
‘modulation’. For now, let’s look at another sound modifier.....
Ring Modulator
The ring modulator is a curious device that
has been around since the early days of electronic
music. It takes two audio inputs and produces the sum and difference frequencies of
those
inputs at the output:
So, for example, if the frequency of the signal at Input X is 440Hz and
the frequency of the
signal at Input Y is 1kHz,
the output will have 1.44kHz and 560Hz - the sum and difference of
the two respectively. Mix in the originals and you have a complex sound comprising
440Hz,
560Hz, 1kHz and 1.44kHz.
Sound processors / modifiers
Page
16

 Loading...
Loading...




