HP 39gII - Page 216

206 Matrices
Examples
Identity Matrix
You can create an identity matrix with the IDENMAT
function. For example, IDENMAT(2) creates the 2×2
identity matrix [[1,0],[0,1]].
You can also create an identity matrix using the MAKEMAT
(make matrix) function. For example, entering
MAKEMAT(I J,4,4) creates a 4 ×
4 matrix showing the
numeral 1 for all elements except zeros on the diagonal.
The logical operator ( ) returns 0 when I (the row
number) and J (the column number) are equal, and returns
1 when they are not equal.
Transposing a
Matrix
The TRN function swaps the row-column and column-row
elements of a matrix. For instance, element 1,2 (row 1,
column 2) is swapped with element 2,1; element 2,3 is
swapped with element 3,2; and so on.
For example, TRN([[1,2],[3,4]]) creates the matrix
[[1,3],[2,4]].
Reduced-Row
Echelon Form
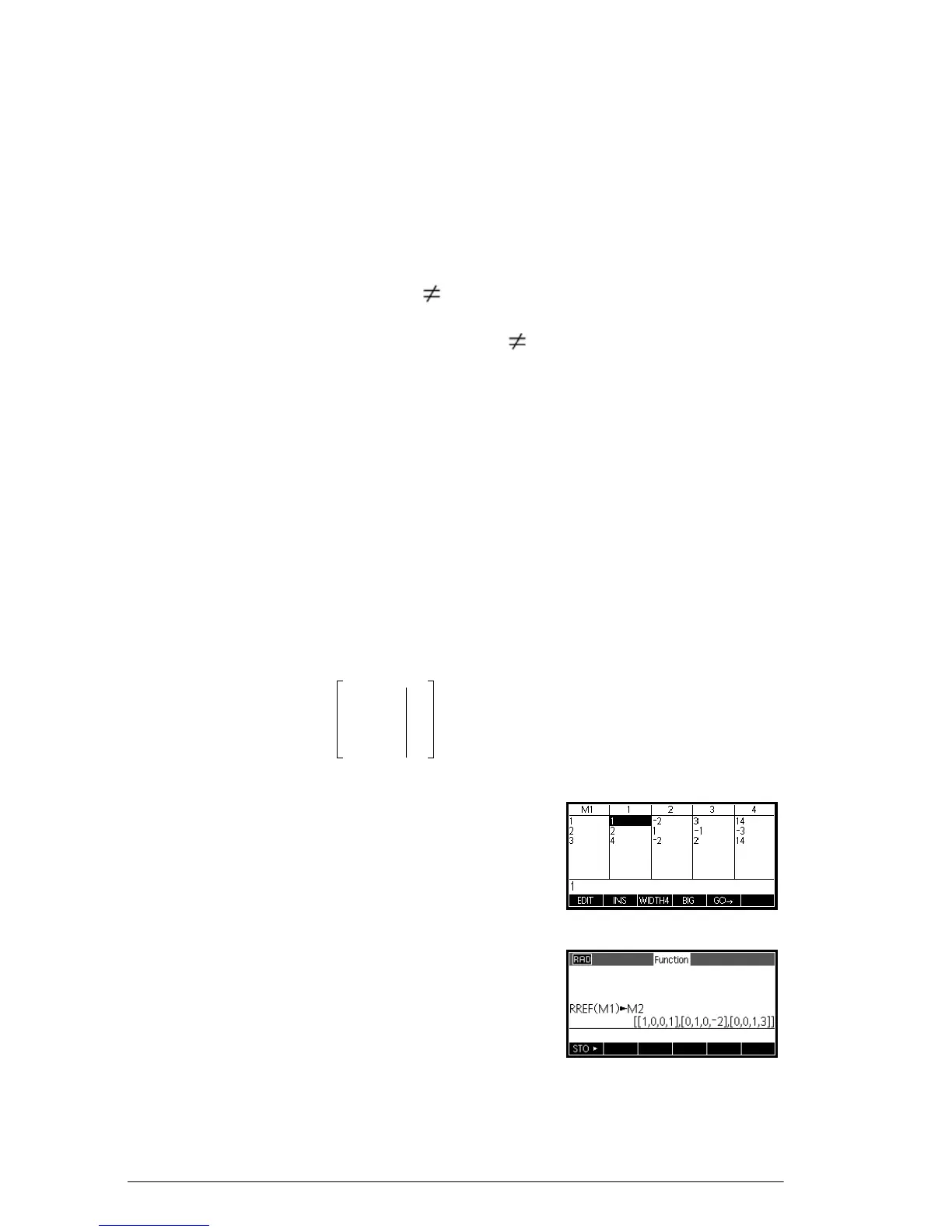
The following set of equations
can be written as the augmented matrix
which can then be stored
as a real matrix in
any matrix variable. M1 is
used in this example.
You can use the RREF
function to change this to
reduced row echelon form,
storing it in any matrix
variable. M2 is used in this
example.
x 2y– 3z+ 14
2xyz–+ 3
4x
–
2y– 2z+ 14
=
=
=
12– 314
21 1– 3–
42– 214
34×