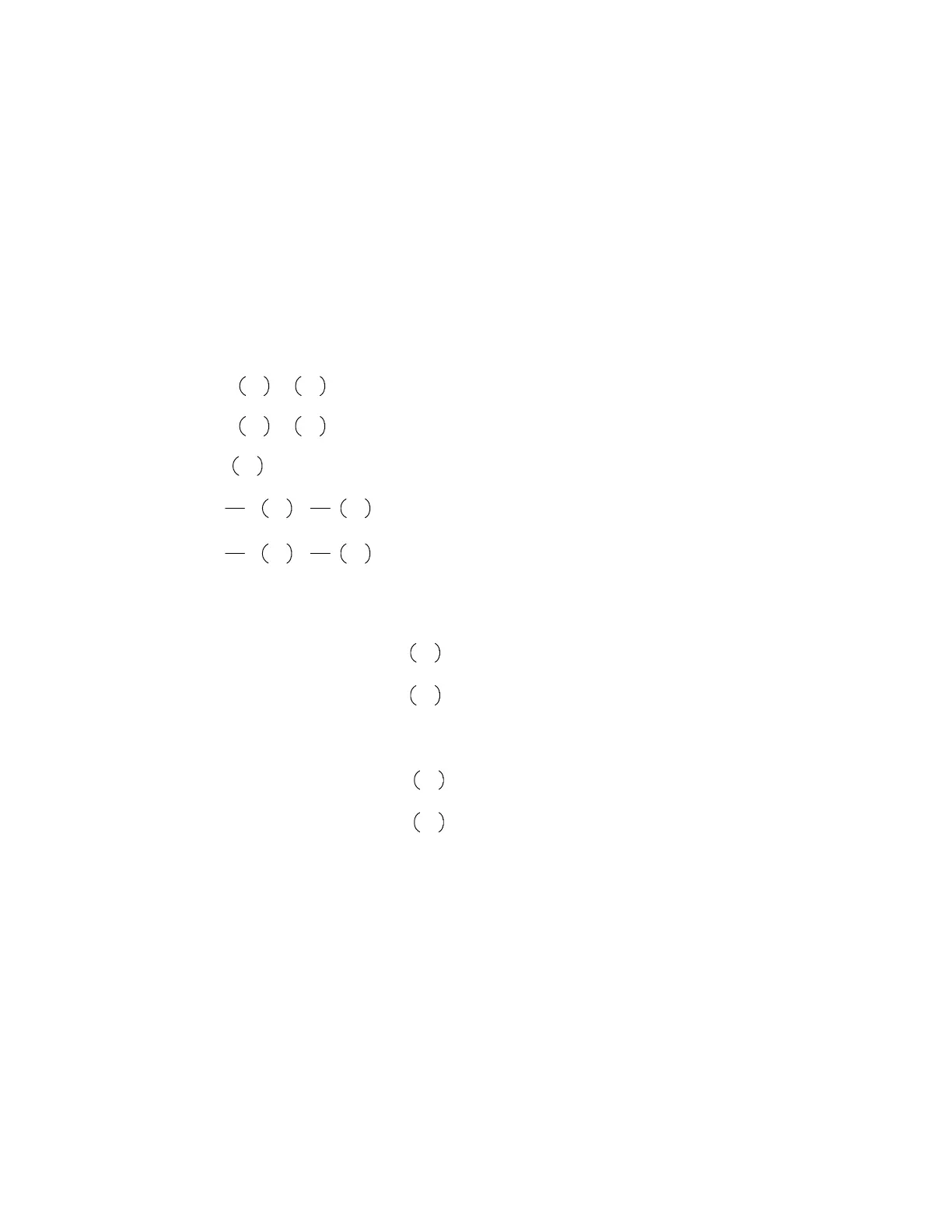s(x) is the splice function
In general, the splice function is [1]
s
(
x
)
= a $ x
4
+ b $ x
3
+ c $ x
2
+ d $ x + e
and the first derivative is [2]
s
∏
(
x
)
= 4 $ a $ x
3
+ 3 $ b $ x
2
+ 2 $ c $ x + d
x
2
is the point between x
1
and x
3
where we specify some desired value for the splice function s(x).
There are several choices for s(x
2
). For example, if f
1
(x) and f
2
(x) intersect, we may want to set x
2
as
the point of intersection, and set s(x
2
) = f
1
(x
2
) = f
2
(x
2
). Alternatively, the splice may work better by
choosing a value for x
2
slightly away from the intersection. If the functions do not intersect on the splice
interval, we may set s(x
2
) between the functions so the splice passes smoothly from one to the other.
We solve for the five coefficients of the splice polynomial by imposing five conditions:
1. The splice matches f
1
at x
1
; there is no discontinuity
f
1
x
1
= s
x
1
2. The splice matches f
2
at x
3
; there is no discontinuity
f
2
x
3
= s
x
3
3. We set the splice value at x
2
to get some desired behavior
s x
2
= y
2
4. Set the first derivatives equal at x
1
for a smooth transition
d
dx
f
1
x
1
=
d
dx
s x
1
5. Set the first derivatives equal at x
3
for a smooth transition
d
dx
f
2
x
3
=
d
dx
s x
3
so we solve these five equations for a, b, c, d and e:
(condition 1) [3]
a $ x
1
4
+ b $ x
1
3
+ c $ x
1
2
+ d $ x
1
+ e = f
1
x
1
(condition 2) [4]
a $ x
3
4
+ b $ x
3
3
+ c $ x
3
2
+ d $ x
3
+ e = f
2
x
3
(condition 3) [5]
a
$
x
2
4
+ b
$
x
2
3
+ c
$
x
2
2
+ d
$
x
2
+ e = y
2
(condition 4) [6]
4
$
a
$
x
1
3
+ 3
$
b
$
x
1
2
+ 2
$
c
$
x
1
+ d = f
1
∏
x
1
(condition 5) [7]
4
$
a
$
x
3
3
+ 3
$
b
$
x
3
2
+ 2
$
c
$
x
3
+ d = f
2
∏
x
3
This set of five equations in five unknowns can sometimes be solved, but just as often they cannot. As
we typically fit the splice over a narrow range of x, a singular matrix error often results from loss of
precision in solving for the coefficients. Even if the singular matrix error does not occur, the solved
coefficients are large and alternating in sign, which means that the polynomial is numerically unstable.
This problem is avoided by finding the splice polynomial as a function of a scaled value of x
s
, instead of
x itself. As usual, proper scaling simplifies the solution. For example, suppose we set x
1s
= -1, x
2s
= 0
and x
3s
= 1, where x
1s
, x
2s
and x
3s
are the scaled values of x
1
, x
0
and x
3
, respectively. The splice
polynomial is now s(x
s
):
[9]
s
(
x
s
)
= a
$
x
s
4
+ b
$
x
s
3
+ c
$
x
s
2
+ d
$
x
s
+ e
Above, we defined h = x
2
- x
1
; now we define a scaled interval half-width h
s
:
6 - 95

 Loading...
Loading...