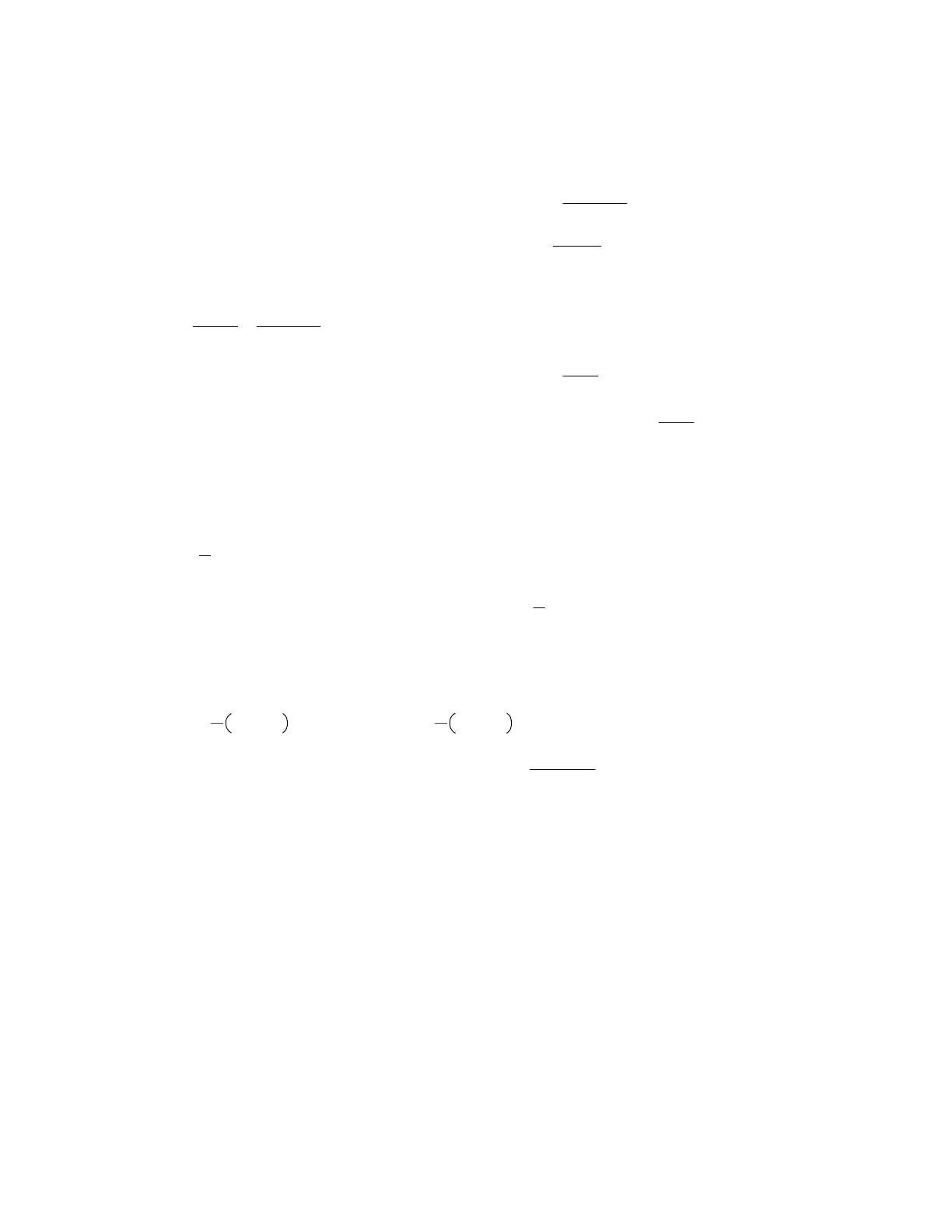[2B]
I = lim
n
d∞
✟
m=1
∞
s
(
x
)
$ ✁
x
m
where [3B]
✁
x
s
m
=
x
sb
−x
sa
n
[4B]
✁
x
m
=
x
b
−x
a
n
Solve [3B] for n, replace in [4B], and define a new variable c such that
[5B]
c =
✁
x
m
✁
x
s
m
=
x
b
−x
a
x
sb
−x
sa
then [6B]
✁
x
s
m
=
✁
x
m
c
Replace [6B] in [1B] for [7B]
Is = lim
n
d∞
✟
m=1
∞
s
s
(
x
s
)
$
✁
x
m
c
Now, since s
s
(xs) = s(x), for any given x and its equivalent scaled x
s
, we move the 1/c constant outside
the sum and limit, and [7B] becomes
I
s
=
1
c
lim
n
d∞
✟
m=1
∞
s
(
x
)
$ ✁
x
m
which, on comparison with [2b], is just
Is =
1
c
$ I
or [8B]
I = c $ I
s
We can also express [8B] in terms of the original scaling factor k. The scaling is defined by
x
sa
=
1
h
x
a
− x
2
x
sb
=
1
h
x
b
− x
2
which we can solve for h:
h =
x
a
−x
b
x
sa
−x
sb
and comparison with [5B] gives
h = c
so we have the final desired result:
I = h
$
I
s
[6.57] Sum binary '1' digits in an integer
Some applications need to find the number of '1' digits in a binary integer. For example, this sum is
needed to calculate a parity bit. Another example would be a game or a simulation in which positions
are stored as '1' digits in an integer, and you need to find the total number of pieces in all positions.
The following TI Basic function will find the number of 1's in the input argument n.
sum1s(n)
Func
©(n) sum of binary 1's in n, n<2^32
©Must use Exact or Auto mode!
©26april02/dburkett@infinet.com
6 - 110
To Next Page
Loading...
Need help?
General
