50 Calculator Keystroke Guide
upper function. To do the shading, at the Home screen press 2nd [DRAW] and select the Shade
command as before. This time, Y1 is the lower function. You may either produce the Y1 character
as before or just type in 2X. Type a comma, and then type in 11 or any other number larger than
Ymax (which is 10 in the Standard viewing window) as the upper function. To see how shading
pattern and density work, type in another comma, followed by –10, 10, 2,3, and a close
parenthesis to complete the command, which should now appear either in the form
Shade(Y1,11,-10,10,2,3) or Shade(2X,11,-10,10,2,3). Press ENTER to graph
the solution of the inequality. The –10 and 10 in the Shade command tell the calculator to begin
the shading on the left at x = –10 (the left edge of the Standard viewing window) and to end the
shading at x = 10 (the right edge of the Standard viewing window), where applicable. The number
2 in the Shade command tells the calculator to use a pattern of horizontal shading. The 3 tells the
calculator to use shading density 3, so only every 3rd row of pixels is shaded.
Use the ClrDraw command as mentioned earlier to erase the shading. Leave xy 2
as Y1 and
enter as Y2 the equation 3
xy . (Be sure to use the negative key (−) in front of the x and the
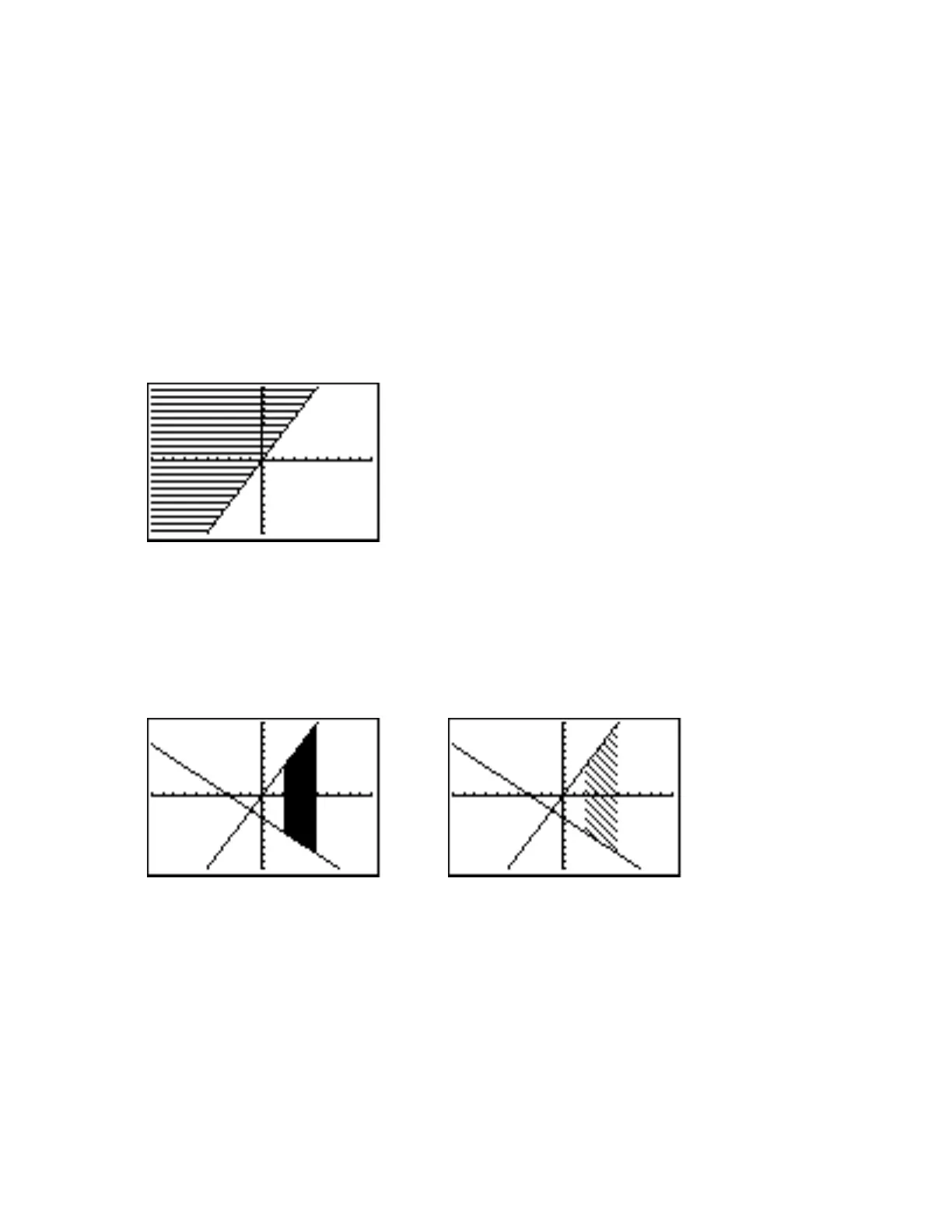
subtraction key in front of the 3.) Suppose you want to solidly shade all points between x = 2 and
x = 5 which lie above Y2 and below Y1. At the Home screen enter the Shade command in this
way: Shade(Y2,Y1,2,5). Press ENTER to see the results. To see a less dense diagonal
shading, first use the ClrDraw command, and then use Shade(Y2,Y1,2,5,3,4).
Shade(Y2,Y1,2,5) Shade(Y2,Y1,2,5,3,4)
You can find more discussion of the Shade command in the TI-83 Graphing Calculator
Guidebook which came with your calculator.
page 295
28 Solve
Your calculator has the ability to solve systems of linear equations by using two matrix concepts
whose full development is beyond the scope of the course you are now taking: matrix
multiplication and the inverse of a matrix. You don’t need to worry about how these concepts
work at this point, since the calculator knows how to do the computations. All you need to be able

 Loading...
Loading...











