MTR-3 Installation Instructions
DEIF A/S Page 17 of 51
Example:
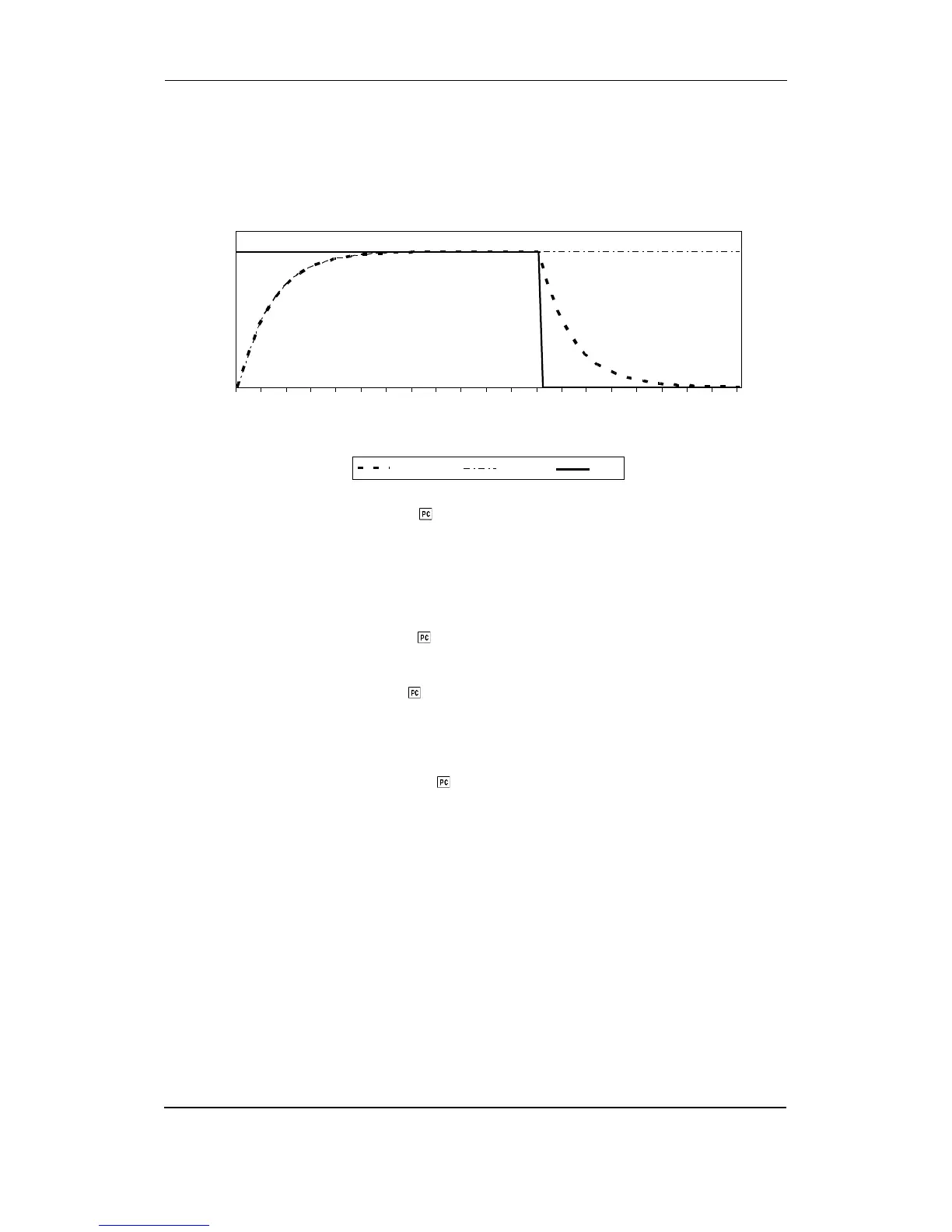
Mode: thermal function
Time constant: 8 min.
Current MD and maximal MD: reset at 0 min.
Starting current for PF and PA (mA)
At all measuring inputs, noise is usually present. It is constant, and its influence on the accuracy
is increased by decreasing measuring signals. It is present also when measuring signals are not
connected, and it occurs at all further calculations as very sporadic measurements. By setting a
common starting current, a limit of input signal is defined where measurements and all other
calculations are still performed.
Starting current for all powers (mA)
Noise is limited with a starting current also at measurements and calculations of powers.
Minimum synchronisation voltage
If all phase voltages are smaller than this (noise limit) setting, the instrument uses current inputs
for synchronisation. If also all phase currents are smaller than Starting current for PF and PA
setting, synchronisation is not possible and frequency displayed is 0.
Reactive power and energy calculation
Two different principles of reactive power and energy calculation are used:
Standard method:
With this method, a reactive power and energy is calculated, based on the assumption that all
power (energy), which is not active, is reactive.
Q
2
= S
2
– P
2
This also means that all higher harmonics will be measured as reactive power (energy).
Delayed current method:
With this method, reactive power (energy) is calculated by multiplication of voltage samples and
delayed current samples (see chapter 8, “Appendix B: Calculations and equations” on page 36):
Q = U × I|
+90°
With this method, reactive power (energy) only represents the true reactive component of
apparent power (energy).

 Loading...
Loading...