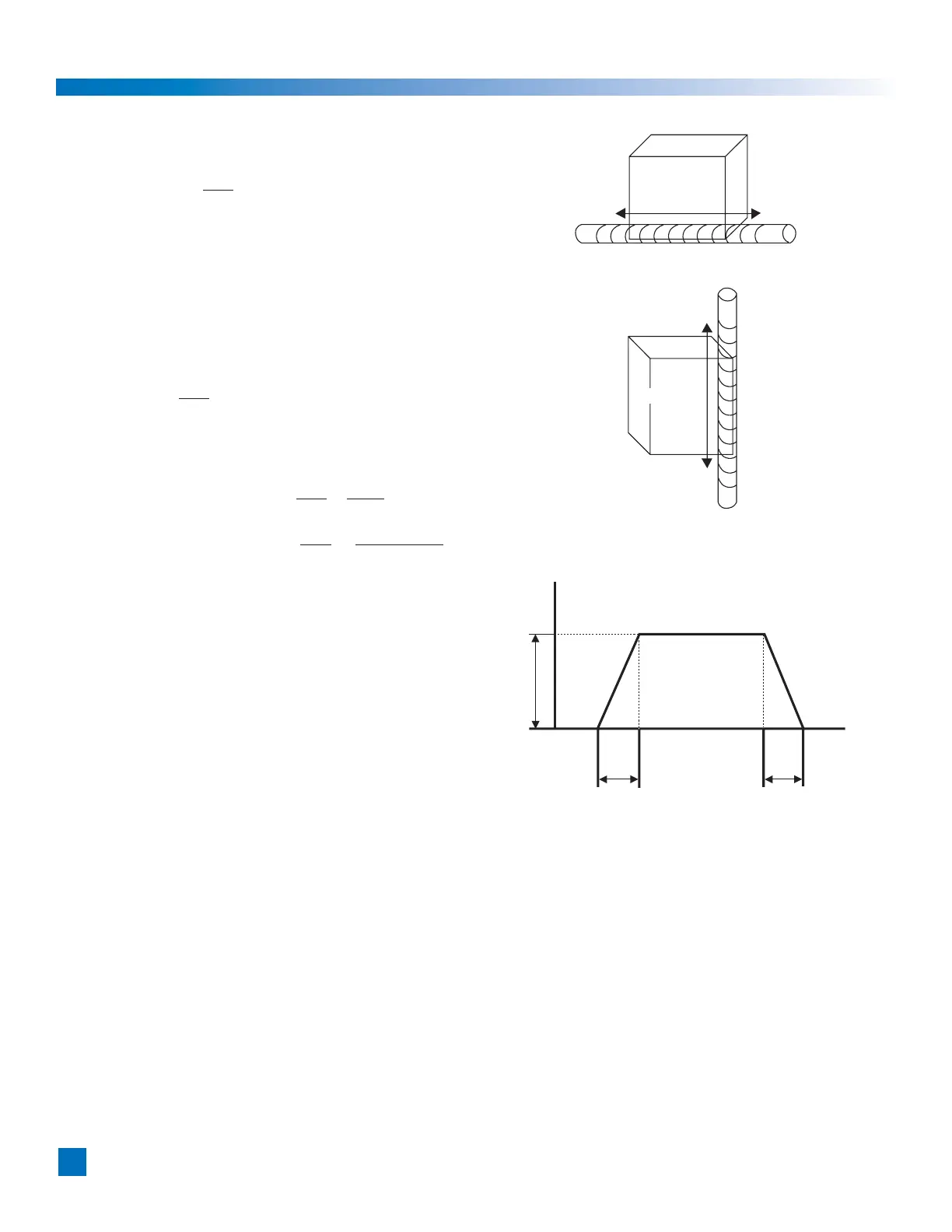
• Horizontal linear motion
The following formula calculates the torque for horizontal
linear motion of mass [W] fed by the screw of pitch [P].
T = 9.8 x μ x W x
P
2 x π
T : torque (N
•m)
μ
: coefficient of friction
W : mass (kg)
P : screw pitch (m)
• Vertical linear motion
The following formula calculates the torque for vertical
linear motion of mass [W] fed by the screw of pitch [P].
T = 9.8 x W x
P
2 x π
2-4-4 Acceleration time and deceleration time
Calculate acceleration and deceleration times for the selected actuator.
Acceleration: ta = (J
A + JL) x
2 x π
x
N
60 T
M – TL
Deceleration: td = (JA + JL) x
2 x π
x
N
60 T
M + 2 x TF – TL
Ta: acceleration time (sec)
T
d: deceleration time (sec)
J
A: actuator inertia (kg•m
2
)
J
L: load inertia (kg•m
2
)
N: actuator speed (r/min)
T
M: maximum torque of actuator (N•m)
T
F: actuator friction torque at max. speed (N•m)
T
F = KT x IM - TM
where, KT: torque constant (N•m/A)
I
M: maximum current (A)
T
L: load torque (N•m)
note that the polarity of the load torque is
plus (+) for counter direction of revolution,
and minus (-) for same direction.
•
Example 1
The load conditions are: Rotary speed: 60r/min
Moment of inertia: 1.5 kg
•m
2
Load torque is so small as to be neglected.
(1) Referring the figure in section 2-1, FHA-25C-50 actuator is selected for the load.
(2) Referring the specification table provided in section 1-4, J
A=0.81 kg•m
2
, TM =150 N•m, KT=22 N•m/A,
and I
M =7.3A are obtained for the FHA-25C-50.
(3) T
F = 22 x 7.3 – 150 = 10.6 N•m is obtained with the formula above.
(4) Acceleration and deceleration times are: ta = (0.81+1.5 ) x 2 x
π
/ 60 x 60 / 150 = 0.097 s
td = (0.81+1.5) x 2 x
π
/ 60 x 60 / (150 + 2 x 10.6) = 0.085 s
(5) If the calculated acceleration times are too long, correct the situation by:
• Reducing load moment of inertia
• Selecting an actuator with a larger frame size
25
Chapter 2 Guidelines for sizing
Mass: W
Mass: W
Pitch: P
Pitch: P
Friction:
Speed
N
Time
ta
td
To Next Page
Loading...
Need help?
General
