45
ρ
ρ
ρ
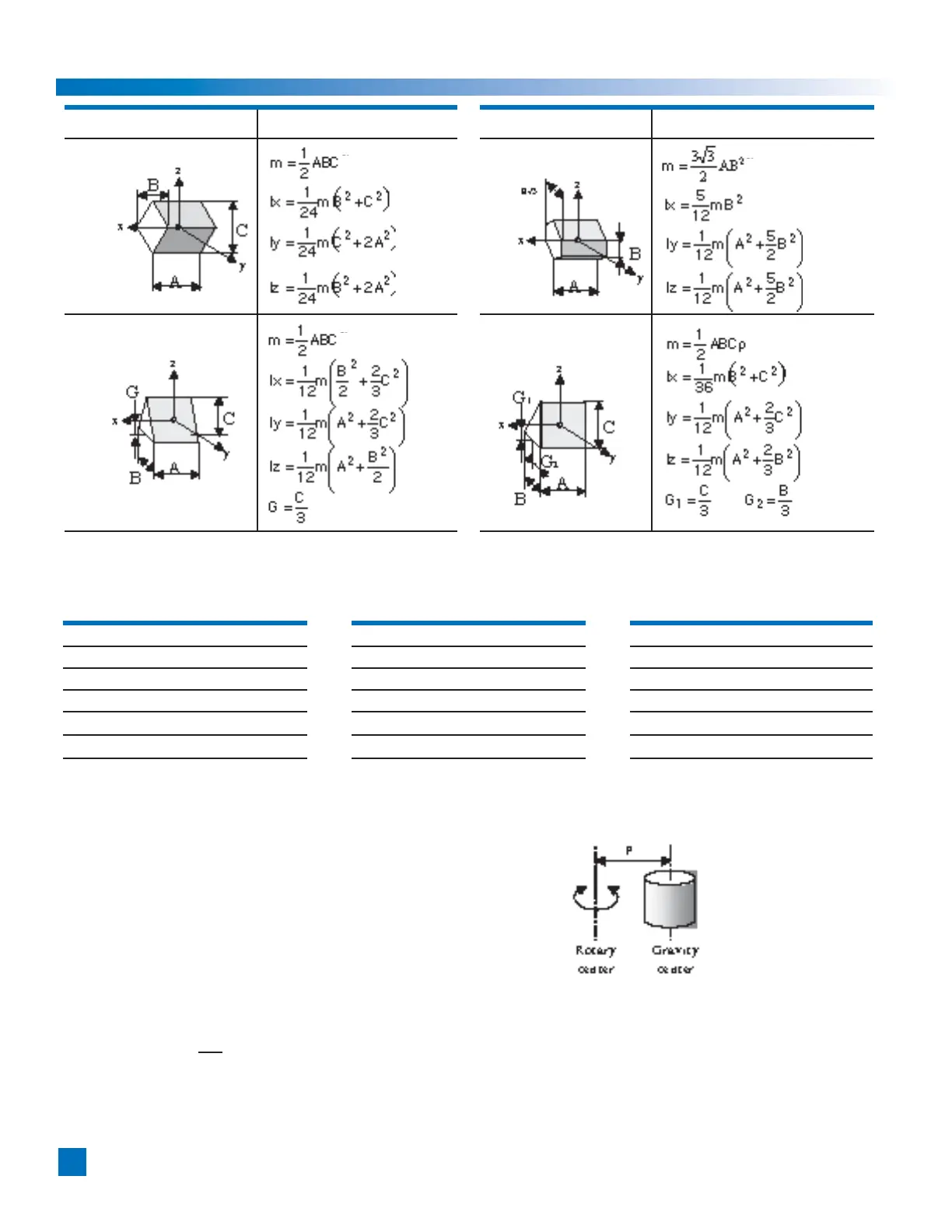
Object form Mass, inertia, gravity center Object form Mass, inertia, gravity center
Rhombus pillar Hexagonal pillar
Isosceles triangle pillar Right triangle pillar
• Example of specific gravity
The following tables show references of specific gravity.
Confirm the specific gravity for the material of the drive load.
Material Gravity Material Gravity Material Gravity
SS45C 7.86 Bronze 8.5 Epoxy resin 1.9
SS41C 7.85 Aluminum 2.7 ABS 1.1
Cast steel 7.85 Duralumin 2.8 Silicon resin 1.8
Cast iron 7.19 Teflon 2.2 Polyurethane rubber 1.25
Copper 8.92 Fluorocarbon resin 2.2 Chloroprene rubber 1.15
(2) Both center lines of rotation and gravity are not the same:
The following formula calculates the moment of inertia when the rotary center is different from the gravity center.
I = I
g + mF
2
I: Inertia when both centers are not the same (kg•m
2
)
I
g: Inertia when both centers are the same (kg•m
2
)
Calculate with formulas described in (1).
m: Mass (kg)
F: Distance between rotary center and gravity center (m)
(3) Inertia of linearly moving objects
The inertia, converted to the actuator axis, of linear moving
objects is calculated with the formula as follows:
I = m
P 2
(
2
π)
I: Inertia of linearly moving objects, converted to the actuator axis (kg•m
2
)
m: Mass (kg)
P: Displacement per one revolution of actuator (m/rev)
Appendix 2 Moment of inertia
To Next Page
Loading...
Need help?
General
