HP 12c Platinum Reference Guide

110 Statistics
Example 1:
A suspect die from a Las Vegas casino is brought to an independent testing
firm to determine its bias, if any. The die is tossed 120 times and the following results
obtained.
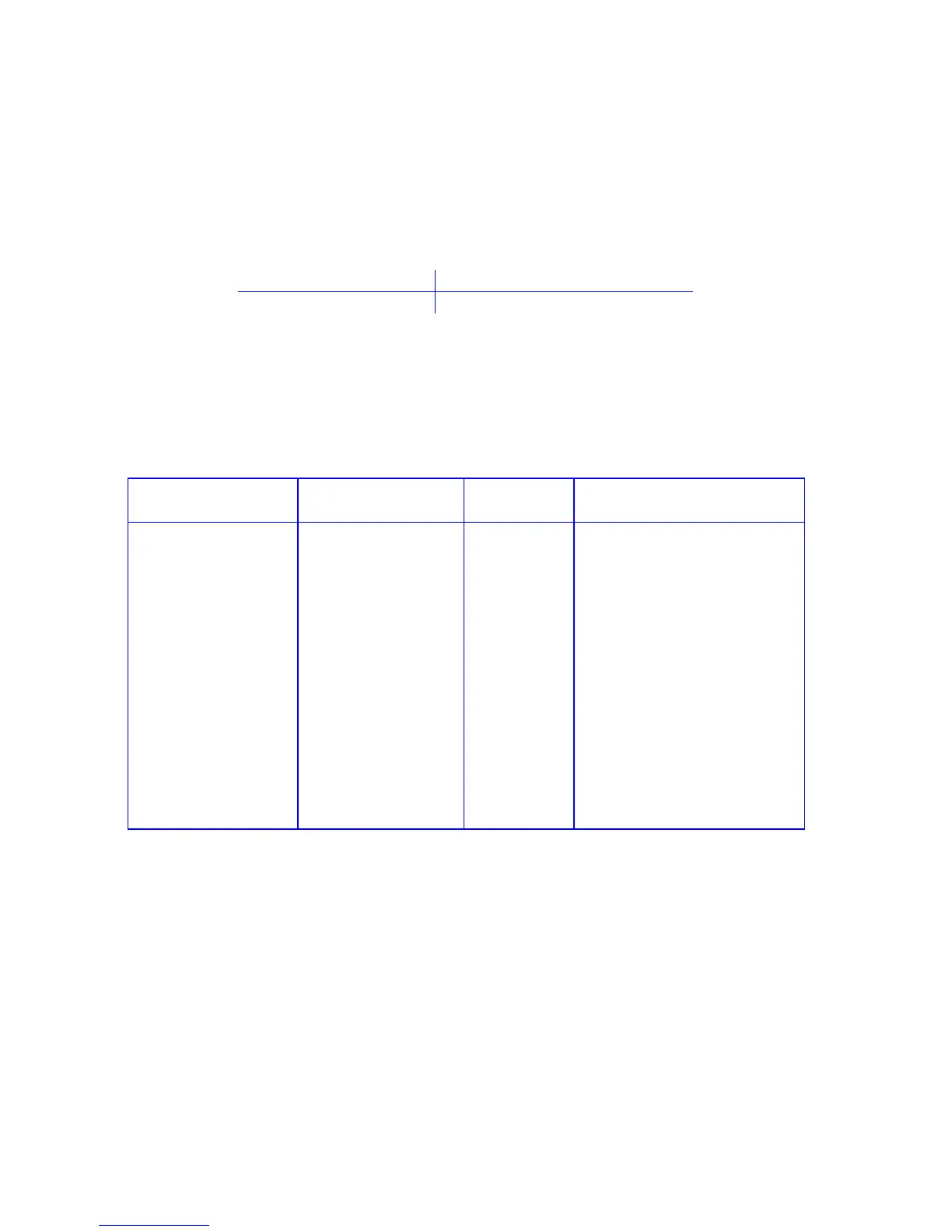
Number 1 2 3 4 5 6
Observed Frequency 25 17 15 23 24 16
The expected frequency = 120 throws / 6 sides, or E = 20 for each number, 1 thru 6.
(Since E is a constant in this example, there is no need to store it in R
0
each time.)
12c platinum / 12C
RPN Keystrokes
12c platinum
ALG Keystrokes
Display Comments
fCLEARH fCLEARH
25\ 25-
20?0-\ 20?0³g’
§:0z+ z:0+~³
1.25
17\20- 17-20³g’
\§:0z+ z:0+~³
1.70
15\20- 15-20³g’
\§:0z+ z:0+~³
2.95
23\20- 23-20³g’
\§:0z+ z:0+~³
3.40
24\20- 24-20³g’
\§:0z+ z:0+~³
4.20
16\20- 16-20³g’
\§:0z+ z:0+~³
5.00
χ
2
The number of degrees of freedom is (n-1). Since n = 6, the degrees of freedom = 5.
Consulting statistical tables, you look up
χ
2
to a 0.05 significance level with 5 degrees of
freedom, and see that
χ
2
0.05,5
= 11.07. Since χ
2
= 5 is within 11.07, we may conclude that
to a 0.05 significance level (probability = .95), the die is fair.
Try the following HP 12C Platinum program with the same example.

HP 12c Platinum Specifications

General

Digits	10 digits
Battery type	CR2032
Type	Financial
Form factor	Pocket

Weight and Dimensions

Weight	110 g
Dimensions (WxDxH)	79 x 129 x 15 mm