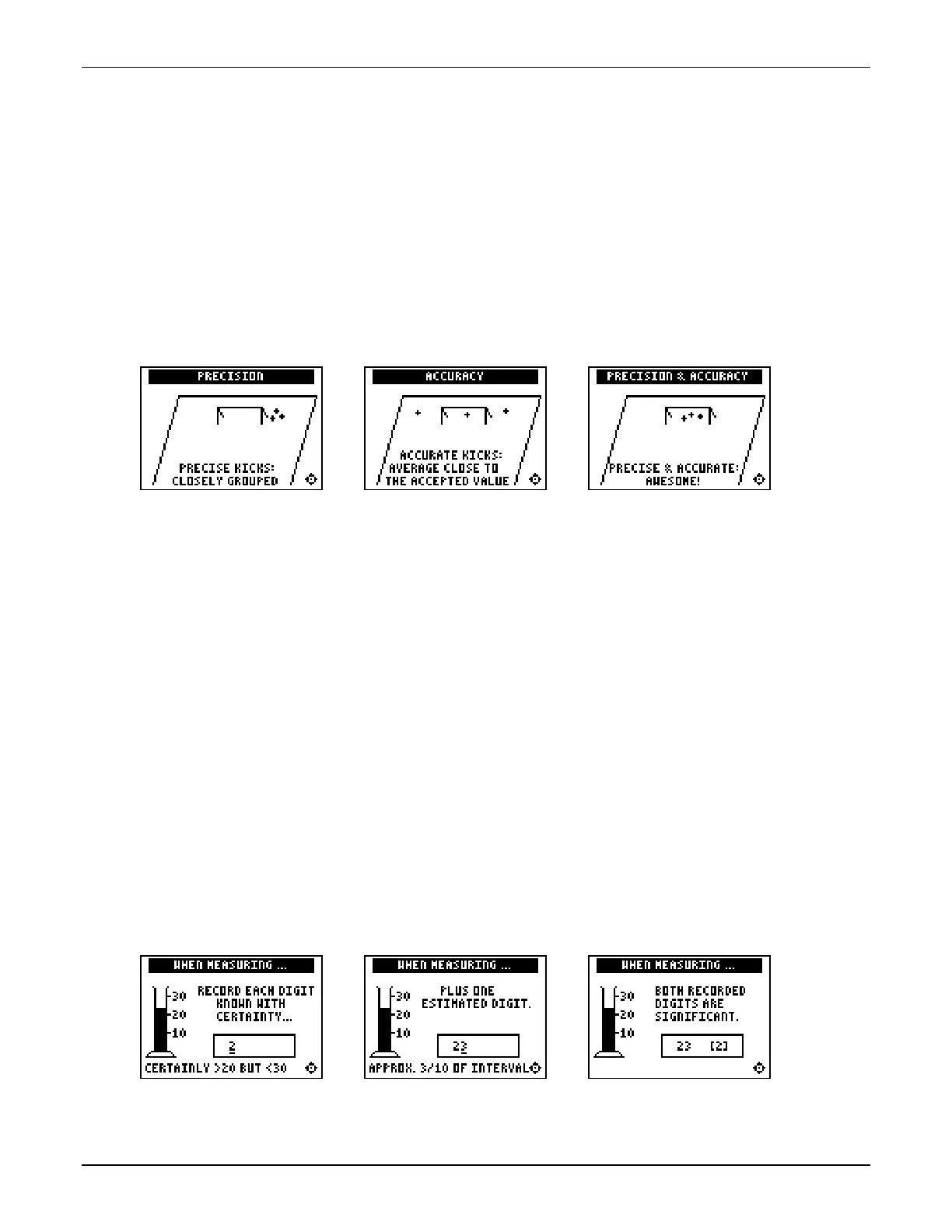
Section 2: Precision & Accuracy
Fundamental Topics in Science © 2001 Texas Instruments Teacher Notes 2-7
Introduction
This section explores the meanings of the terms precise and accurate. Notice the analogy of
precision and accuracy of measurements to that of three sets of soccer kicks. Point out that:
•
High precision results in closely grouped, repeatable values (but not necessarily near the
accepted standard).
•
High accuracy results in values whose average is near the accepted standard (although
individual values may differ widely).
•
Obviously, both high precision and high accuracy are desirable. Precision is often preferable
in measuring instruments. Since precise results are highly predictable, a correction can be
applied using a process known as calibration so that the net result is made accurate.
Extension
Point out to students that while both high precision and high accuracy are desirable, this is not
always possible. These are possible work-group discussion topics.
•
Ask, “If your team could kick precisely or accurately, but not both, which would you prefer,
and why?” Tell them to explain their reason in writing. Some students might say, “Accurately,
because we’d stand the best chance of getting at least one score.” But others might say,
“Precisely, because the goal is to win the game. If both teams were equally accurate, it might
be a tie. Only with high precision would you stand the chance of a big win.” They would
certainly have a case!
•
Ask students to describe what might be the effects of high accuracy, but low precision, for
situations such as a political election, determining the age of artifacts from an archaeological
dig, or taking a population census. Then ask them to describe what might be the effects of
high precision, but low accuracy, for the same situations.
Concepts
This section explores proper recording practices and significant figures.
Remind students that, when reading a measuring instrument, it is standard laboratory practice to
report all the certain digits (limited by the instrument’s finest divisions) plus the first estimated
digit.
 Loading...
Loading...











