HEIDENHAIN TNC 426 B

HEIDENHAIN TNC 426 B, TNC 430 257
The TNC displays the following program blocks:
16 FN0: Q5 = +10
17 FN3: Q12 = +Q5 * +7
10.4 Trigonometric Functions
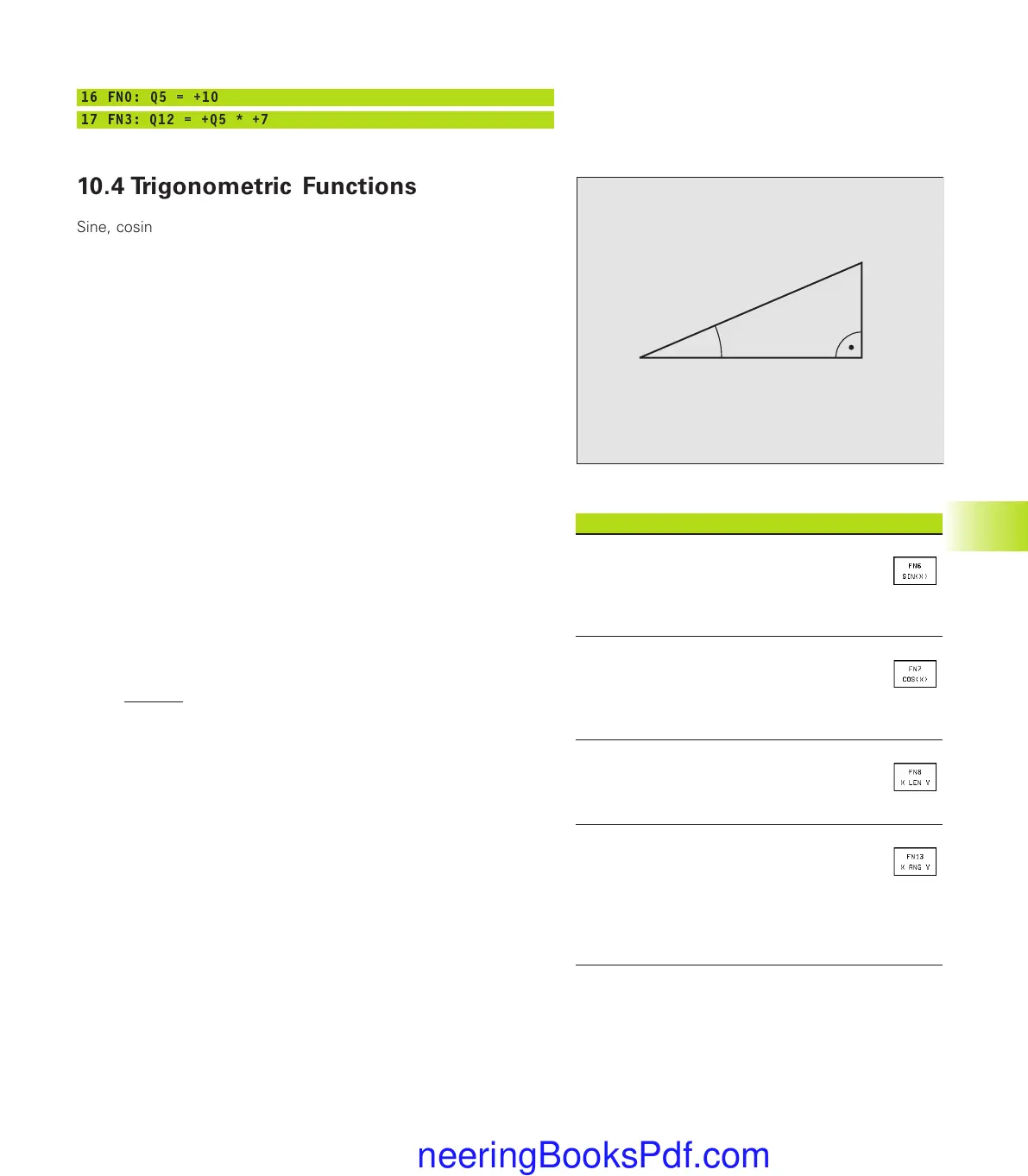
Sine, cosine and tangent are terms designating the ratios of sides
of right triangles. For a right triangle, the trigonometric functions of
the angle a are defined by the following equations:
Sine: sin α =a / c
Cosine: cos α =b / c
Tangent: tan α = a / b = sin α / cos α
where
■
c is the side opposite the right angle
■
a is the side opposite the angle a
■
b is the third side.
The TNC can find the angle from the tangent
α = arctan α = arctan (a / b) = arctan (sin α / cos α)
Example:
a=10 mm
b=10 mm
α = arctan (a / b) = arctan 1 = 45°
Furthermore:
a
2
+ b
2
= c
2
(where a
2
= a x a)
c = √ (a
2
+ b
2
)
Programming trigonometric functions
Press the TRIGONOMETRY soft key to call the trigonometric
functions. The TNC then displays the soft keys that are listed in the
table at right.
Programming: compare „Example: Programming
fundamental operations“.
b
c
a
α
Function Soft key
FN6: SINE
Example: FN6: Q20 = SIN–Q5
Calculate the sine of an angle in
degrees (°) and assign it to a parameter.
FN7: COSINE
Example: FN7: Q21 = COS–Q5
Calculate the cosine of an angle in
degrees (°) and assign it to a parameter.
FN8: ROOT-SUM OF SQUARES
Example: FN8: Q10 = +5 LEN +4
Calculate and assign length from two values
FN13: ANGLE
Example: FN13: Q20 = +10 ANG–Q1
Calculate the angle from the arc tangent
of two sides or from the sine and cosine
of the angle (0 < angle < 360°) and
assign it to a parameter.
10.4 Trigonometric Functions
MKAP10.PM6 30.06.2006, 07:04257
www.EngineeringBooksPdf.com