Carel EVD4 User Manual

41
PID
d
u
y°
y
+
+
P(s)
n
w
+
+
Fig. 1
PID
d
+
+
P(s)
n
+
+
A
B D
E
C
Fig. 2
ENGLISH
EVD
4
+030220227 - rel. 2.1 - 12.06.2008
APPENDIX IV. SUMMARY OF PID CONTROL
IV.I Symbols used
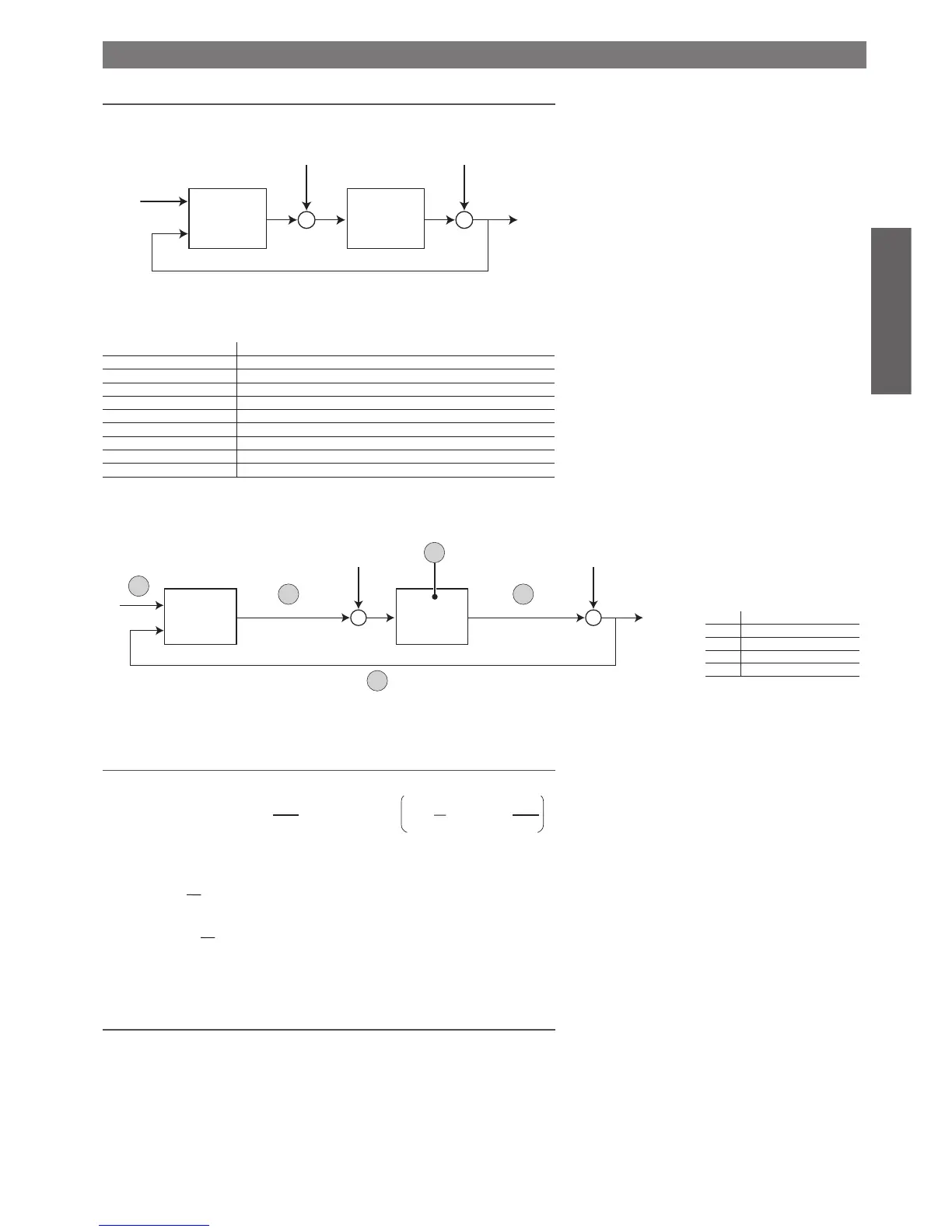
In this introduction to PID control, reference is made to the following block diagram, which is a simpli-
fi ed representation of an cycle control individual:
With the following symbols:
symbol meaning
y°(t) Reference signal or set point
w(t) Controlled or process variable
y(t) Value of the controlled or process variable
e(t) Error, defi ned as e(t)=y°(t)-y(t)
u(t) Control variable
d(t) Load disturbance
n(t) Measurement noise
PID PID control
P(s) Transfer function describing the process being controlled
If the PID control manages the superheat value by positioning the electronic expansion valve, which we
have called the SH PID, then:
IV.II Pid control law
PID control in its simplest form is defi ned by the following law
u(t)= K
p
e(t) + K
i
∫e(t)dt + K
d
de(t)
dt T
i
oppure
u(t)= K e(t) +
1
∫e(t)dt + T
d
de(t)
dt
This means that the control is calculated as the sum of three contributions:
P or proportional action
Ke(t)
(k = proportional gain)
I or integral action
T
i
K
∫e(t)d
t
(Ti = integral time)
D or derivative action
T
i
K
∫e(t)d
t
(Td = derivative time)
hence the defi nition ‘PID control’.
IV.III Proportional action
EFFECT OF K
Increasing the value of the proportional gain, increases the reactivity of the valve, to the limit
where this may cause instability and not reach the set point with precision. This depends on the
ratio between the circuit capacity and the valve capacity, and on the maximum number of valve
control steps.
The proportional action guarantees control over the process variable that is proportional to the system
error at the instant t. The controller performs a corrective action on the control variable, at the instant t,
that is equal to u(t)=K*e(t)= K*(y(t)-y0(t)).
The proportional action follows the logic whereby the greater the error, instant by instant, the more
Key
A y° (t)= SH set piont
B u (t)= valve position
C lamination process
D w (t)= real SH
E y (t)= measured SH

Carel EVD4 Specifications

General

Brand	Carel
Model	EVD4
Category	Controller
Language	English