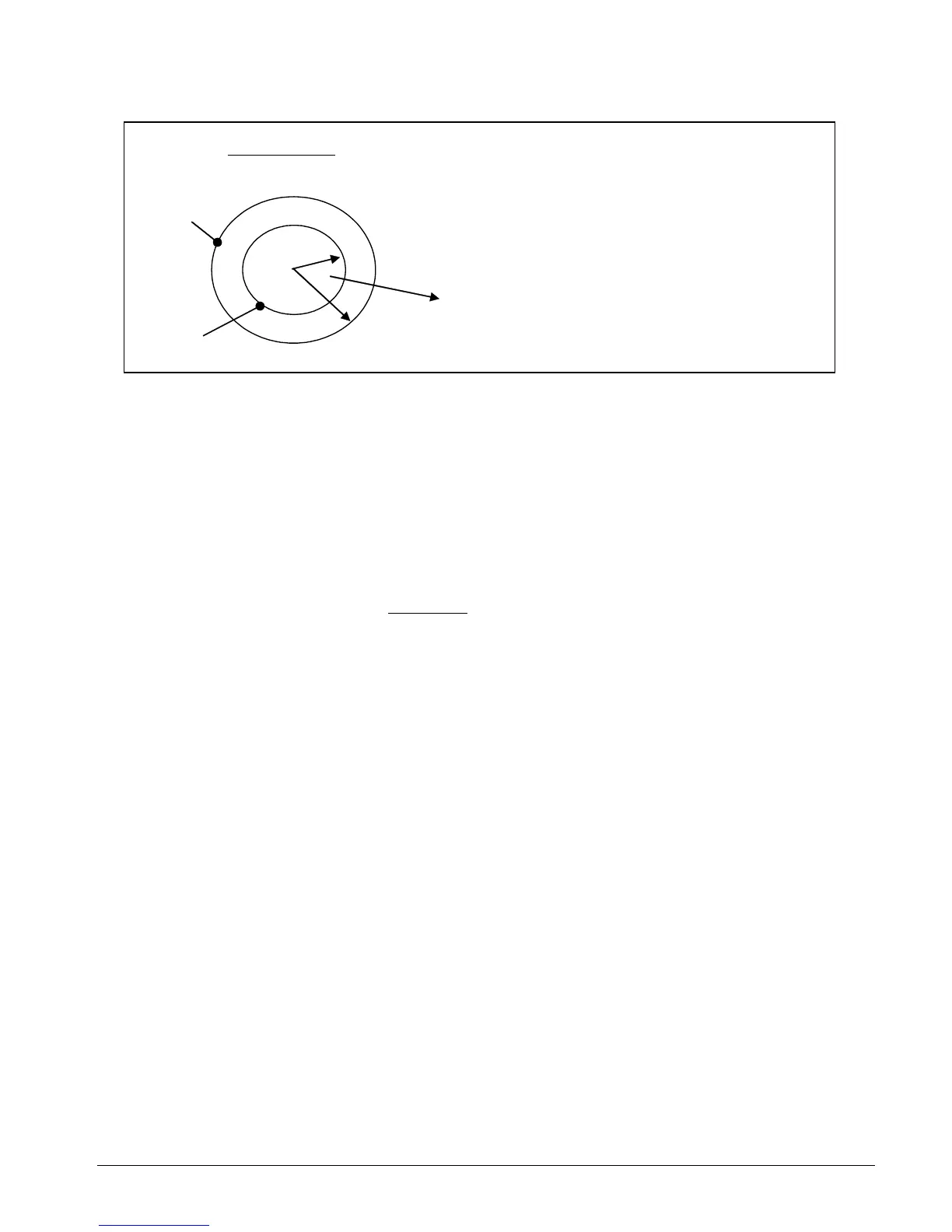
b. Through a Hollow Cylinder With Internal Radius, r1 and External Radius, r2
Q = 2
π
kL (T1 - T2)
where L is the length of the cylinder
ln (r2/r1) T1 is the internal surface temperature
T2 is the external surface temperature
T2 with T1 > T2
Heat transfer, Q
r2
T1
r1
The piping insulation can be considered as a hollow cyclinder and the above formula may be
used in calculating the insulation thickness.
When the heat flux has conducted through the thickness of the pipe insulation, the heat will then
dissipate at the external surface by means of convection.
The heat transfer rate by convection (Qc) from a surface with temperature T can be expressed as:
Qc = hA(T - Ta) where Ta is the ambient air temperature
A is the surface area
By equating the conductive and convective heat transfer equations, it can be shown:
r1 * ln (r2/r1) = k (T1 - T2)
h (T2 - Ta)
Therefore, with the known k-value and h-value, together with the pipe size (r1) and operating
temperature T1, we can calculate the external radius, r2, to obtain a specified external surface
temperature, T2.
a) We can thus calculate the minimum required insulation thickness to ensure a safe external
surface temperature to protect from the hot water pipe temperature.
b) We can also calculate the minimum required insulated thickness to prevent condensation
by ensuring the external surface temperature is not lower than the dew point temperature
of the air surrounding the piping.
Refer to Appendix 12 for a psychometric chart to determine the dew point temperature for
different temperatures and humidity levels.
Section 7 Page 95
 Loading...
Loading...