Theory of thermography
34
The spectral emissivity ε
λ
= the ratio of the spectral radiant power from an object to that
from a blackbody at the same temperature and wavelength.
Expressed mathematically, this can be written as the ratio of the spectral emittance of the
object to that of a blackbody as follows:
Generally speaking, there are three types of radiation source, distinguished by the ways in
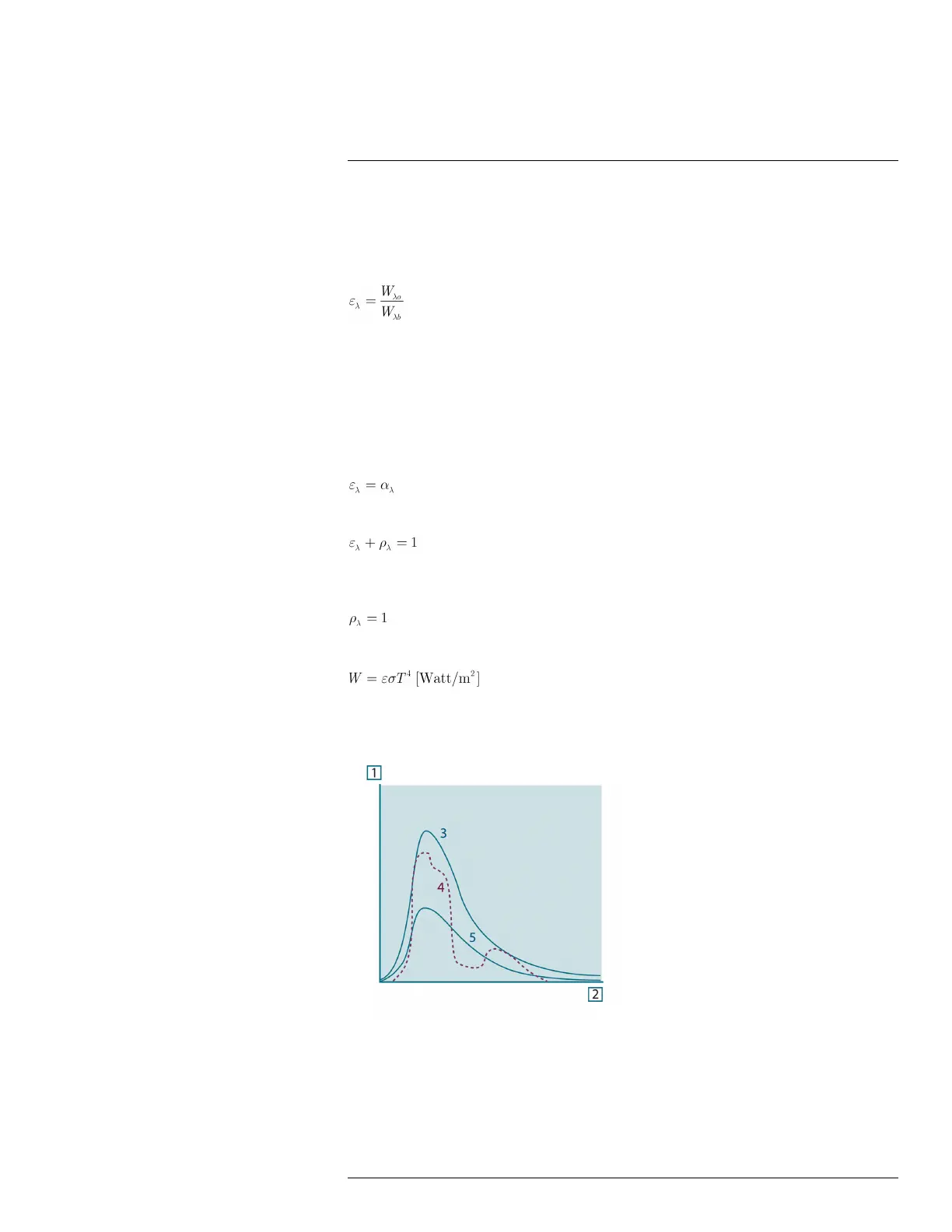
which the spectral emittance of each varies with wavelength.
• A blackbody, for which ε
λ
= ε = 1
• A graybody, for which ε
λ
= ε = constant less than 1
• A selective radiator, for which ε varies with wavelength
According to Kirchhoff’s law, for any material the spectral emissivity and spectral absorp-
tance of a body are equal at any specified temperature and wavelength. That is:
From this we obtain, for an opaque material (since α
λ
+ ρ
λ
= 1):
For highly polished materials ε
λ
approaches zero, so that for a perfectly reflecting material
(i.e. a perfect mirror) we have:
For a graybody radiator, the Stefan-Boltzmann formula becomes:
This states that the total emissive power of a graybody is the same as a blackbody at the
same temperature reduced in proportion to the value of ε from the graybody.
Figure 34.8 Spectral radiant emittance of three types of radiators. 1: Spectral radiant emittance; 2: Wave-
length; 3: Blackbody; 4: Selective radiator; 5: Graybody.
#T559879; r. AO/35410/35410; en-US
187
 Loading...
Loading...