HP 15c Collector's Edition User Manual

220
Appendix D
A Detailed Look at _
Section 13, Finding the Roots of an Equation, includes the basic
information needed for the effective use of the _ algorithm. This
appendix presents more advanced, supplemental considerations
regarding _.
How _ Works
You will be able to use _ most effectively by having a basic
understanding of how the algorithm works.
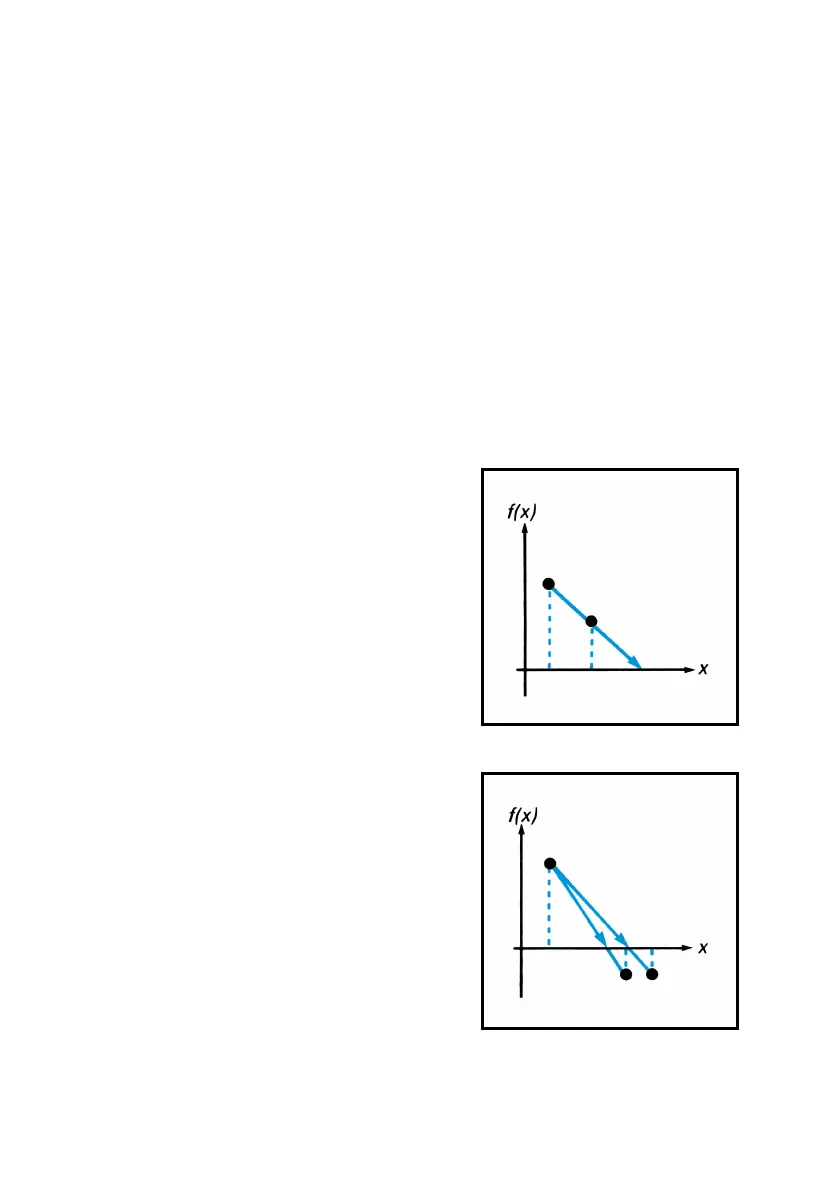
In the process of searching for a zero of the
specified function, the algorithm uses the
value of the function at two or three
previous estimates to approximate the
shape of the function’s graph. The
algorithm uses this shape to intelligently
“predict” a new estimate where the graph
might cross the x-axis. The function
subroutine is then executed, computing the
value of the function at the new estimate.
This procedure is performed repeatedly by the _ algorithm.
If any two estimates yield function values
with opposite signs, the algorithm
presumes that the function’s graph must
cross the x-axis in at least one place in the
interval between these estimates. The
interval is systematically narrowed until a
root of the equation is found.
A root is successfully found either if the
computed function value is equal to zero or
if two estimates, differing by one unit in
their last significant digit, give function values having opposite signs. In
this case, execution stops and the estimate is displayed.

HP 15c Collector's Edition Specifications

General

Model	HP 15c Collector's Edition
Category	Calculator
Type	Scientific
Power Source	Battery
Manufacturer	HP
Display	LCD
Functions	complex numbers, matrix operations

Summary

Introduction

This Handbook

Outlines the structure of the manual, detailing its parts and how to use it for learning.

The HP Community

Discusses user groups and websites for HP calculator enthusiasts and information sharing.

Part I: HP 15c Fundamentals

Section 1: Getting Started

Covers basic operations like powering on, keyboard layout, and primary/alternate functions.

Section 2: Numeric Functions

Explains essential numeric operations including logs, trig, powers, and conversions.

Section 3: The Automatic Memory Stack, LAST X, and Data Storage

Details the RPN stack, LAST X register, and data storage operations.

Part II: HP 15c Programming

Section 6: Programming Basics

Introduces core programming concepts: creating, loading, running programs, and memory.

Section 8: Program Branching and Controls

Covers controlling program flow using branching, loops, and conditional tests.

Part III: HP 15c Advanced Functions

Section 11: Calculating With Complex Numbers

Covers entering, manipulating, and performing calculations with complex numbers.

Section 12: Calculating With Matrices

Explains matrix operations, including dimensioning, element access, and calculations.

Section 13: Finding the Roots of an Equation

Details using the SOLVE function for numerical root finding and equation solving.

Section 14: Numerical Integration

Explains how to perform numerical integration using the ∫f(x)dx key and subroutines.

Appendix A: Error Conditions

Error 8: No Root

Explains the error when the SOLVE function cannot find a root.

Error 0: Improper Mathematics Operation

Lists and explains errors related to mathematical operations and illegal arguments.

Appendix D: A Detailed Look at SOLVE

How SOLVE Works

Explains the numerical technique and logic behind the SOLVE algorithm.

Finding Several Roots

Discusses methods for finding multiple roots of an equation using the SOLVE function.