230 Appendix D: A Detailed Look at _
If the algorithm terminates its search near
a local minimum of the function’s
magnitude, clear the
Error 8
display and
observe the numbers in the X-, Y-, and Z-
registers by rolling down the stack. If the
value of the function saved in the Z-register
is relatively close to zero, it is possible that
a root of your equation has been found—
the number returned in the X-register may
be a 10-digit number very close to a
theoretical root. You can explore this
potential minimum further by rolling the stack until the returned
estimates are back in the X- and Y-registers and then executing _
again using these numbers as initial estimates. If an actual minimum has
been found,
Error 8
will again be displayed and the number in the X-
register will be approximately the same as before, but possibly closer to
the actual location of the minimum.
Of course, you may deliberately use _ to find the location of a local
minimum of the function’s magnitude. However, in this case you must be
careful to confine the search in the region of the minimum. Remember,
_ tries hard to find a zero of the function.
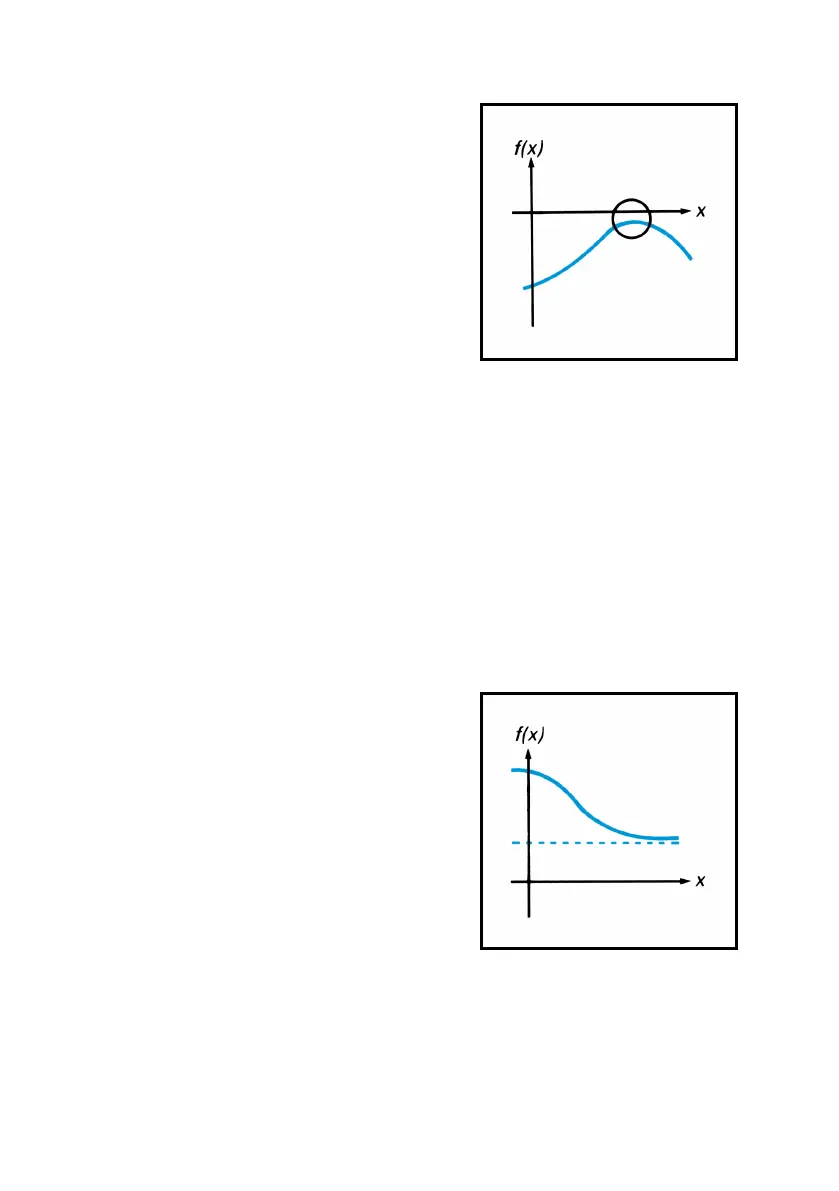
If the algorithm stops searching and
displays
Error 8
because it is working on a
horizontal asymptote (when the value of
the function is essentially constant for a
large range of x), the estimates in X- and Y-
registers usually are significantly different
from each other. The number in the Z-
register is the value of the potential
asymptote. If you execute _ again
using as initial estimates the numbers that
were returned in the X- and Y-registers, a
horizontal asymptote may again cause
Error 8
, but with numbers in the
X- and Y-registers that will differ from the previous numbers. The value
of the function in the Z-register would then be about the same as that
obtained previously.

 Loading...
Loading...