Appendix D: A Detailed Look at _ 237
Keystrokes Display
l 2
036- 45 2
-
037- 30
Deflation for third root.
÷
038- 10
Find the fourth root.
| ¥
-1.0929 -07
10 ” v
-10.0000
Same initial estimates.
20 ”
-20
´ _ 2
8.5001
Fourth root.
O 3
8.5001
Stores root for
reference.
) )
-0.0009
Deflated function value
near zero.
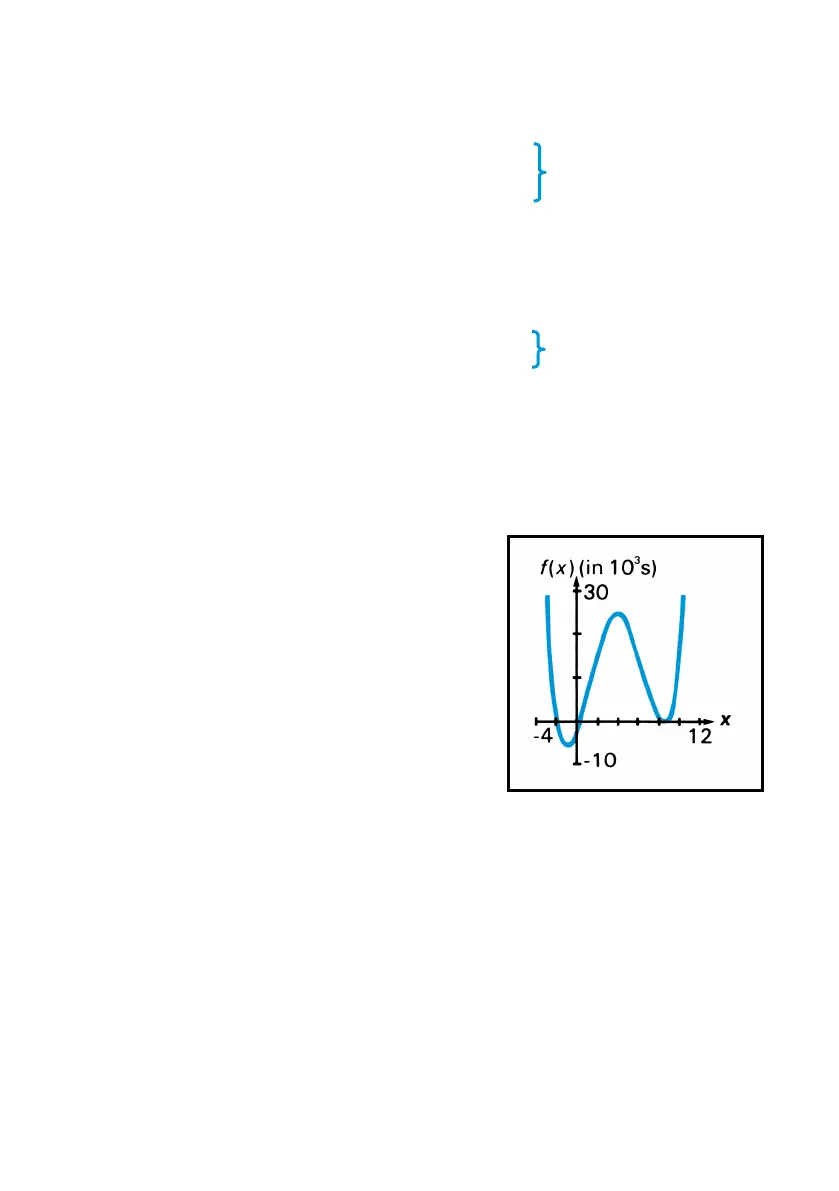
Using the same initial estimates each
time, you have found four roots for this
equation involving a fourth-degree
polynomial. However, the last two roots
are quite close to each other and are
actually one root (with a multiplicity of
2). That is why the root was not
eliminated when you tried deflation
once at this root. (Round-off error
causes the original function to have
small positive and negative values for
values of x between 8.4999 and 8.5001;
for x = 8.5 the function is exactly zero.)
In general, you will not know in advance the multiplicity of the root you
are trying to eliminate. If, after you have attempted to eliminate a root,
_ finds that same root again, you can proceed in a number of ways:
Use different initial estimates with the deflated function in an
attempt to search for a different root.
Use deflation again in an attempt to eliminate a multiple root. If you
do not know the multiplicity of the root, you may need to repeat this
a number of times.
Graph of f (x)
To Next Page
Loading...
Need help?
General
