HP 15c Collector's Edition User Manual

250 Appendix E: A Detailed Look at f
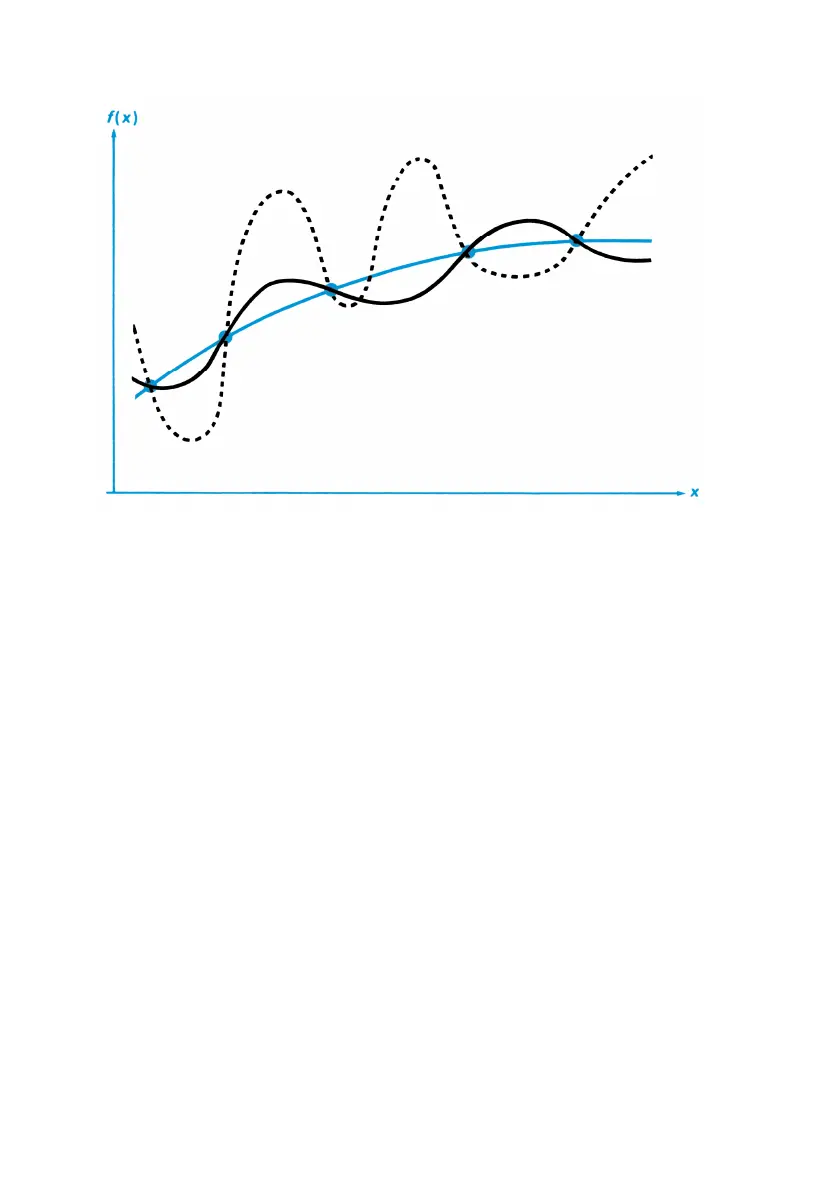
With this number of sample points, the algorithm will calculate the same
approximation for the integral of any of the functions shown. The actual
integrals of the functions shown with solid lines are about the same, so
the approximation will be fairly accurate if f (x) is one of these functions.
However, the actual integral of the function shown with a dashed line is
quite different from those of the others, so the current approximation will
be rather inaccurate if f (x) is this function.
The f algorithm comes to know the general behavior of the function by
sampling the function at more and more points. If a fluctuation of the
function in one region is not unlike the behavior over the rest of the
interval of integration, at some iteration the algorithm will likely detect
the fluctuation. When this happens, the number of sample points is
increased until successive iterations yield approximations that take into
account the presence of the most rapid, but characteristic, fluctuations.
For example, consider the approximation of


0
xe
−x
dx .

HP 15c Collector's Edition Specifications

General

Model	HP 15c Collector's Edition
Category	Calculator
Type	Scientific
Power Source	Battery
Manufacturer	HP
Display	LCD
Functions	complex numbers, matrix operations

Summary

Introduction

This Handbook

Outlines the structure of the manual, detailing its parts and how to use it for learning.

The HP Community

Discusses user groups and websites for HP calculator enthusiasts and information sharing.

Part I: HP 15c Fundamentals

Section 1: Getting Started

Covers basic operations like powering on, keyboard layout, and primary/alternate functions.

Section 2: Numeric Functions

Explains essential numeric operations including logs, trig, powers, and conversions.

Section 3: The Automatic Memory Stack, LAST X, and Data Storage

Details the RPN stack, LAST X register, and data storage operations.

Part II: HP 15c Programming

Section 6: Programming Basics

Introduces core programming concepts: creating, loading, running programs, and memory.

Section 8: Program Branching and Controls

Covers controlling program flow using branching, loops, and conditional tests.

Part III: HP 15c Advanced Functions

Section 11: Calculating With Complex Numbers

Covers entering, manipulating, and performing calculations with complex numbers.

Section 12: Calculating With Matrices

Explains matrix operations, including dimensioning, element access, and calculations.

Section 13: Finding the Roots of an Equation

Details using the SOLVE function for numerical root finding and equation solving.

Section 14: Numerical Integration

Explains how to perform numerical integration using the ∫f(x)dx key and subroutines.

Appendix A: Error Conditions

Error 8: No Root

Explains the error when the SOLVE function cannot find a root.

Error 0: Improper Mathematics Operation

Lists and explains errors related to mathematical operations and illegal arguments.

Appendix D: A Detailed Look at SOLVE

How SOLVE Works

Explains the numerical technique and logic behind the SOLVE algorithm.

Finding Several Roots

Discusses methods for finding multiple roots of an equation using the SOLVE function.