HP 40gs - Page 301

Step-by-Step Examples 16-27
Solution 1
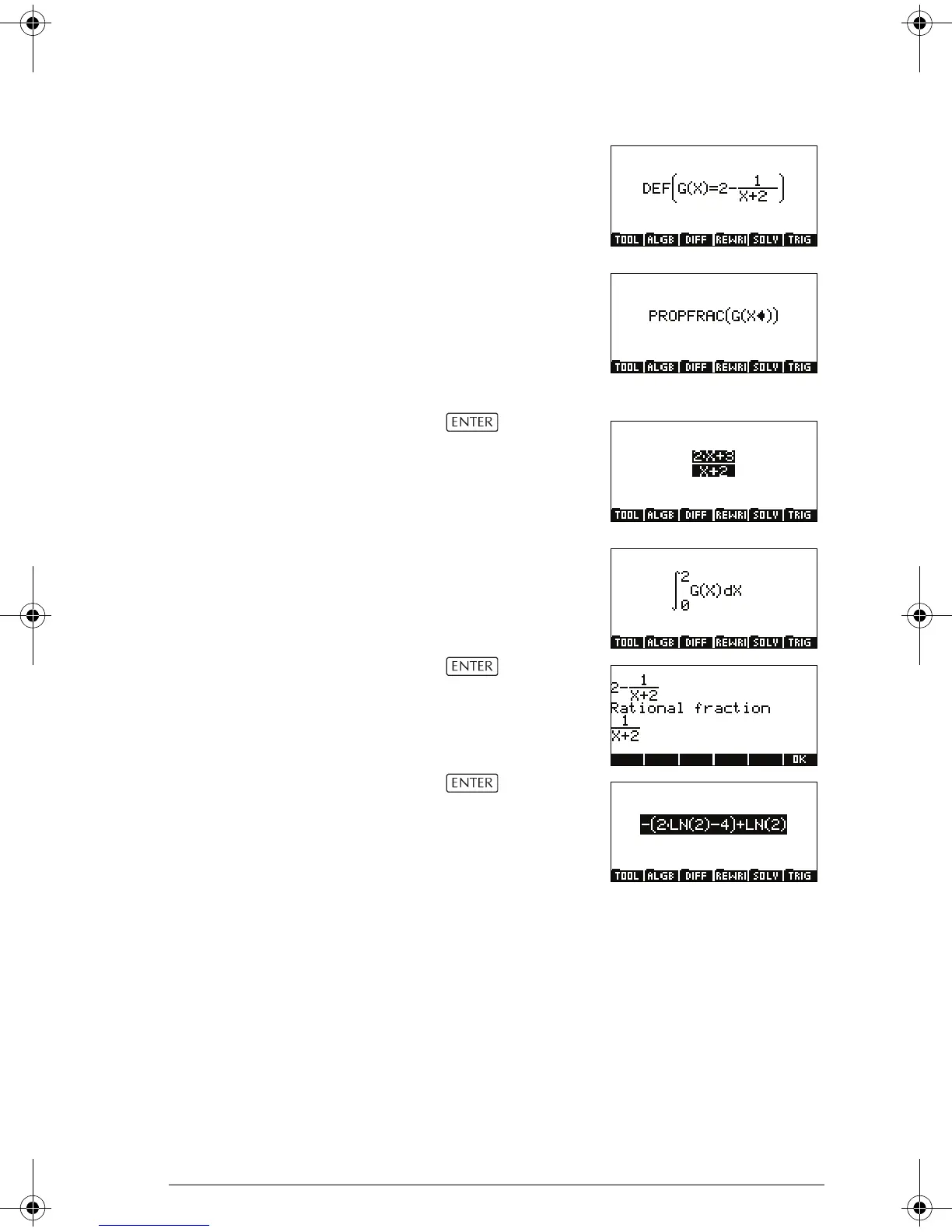
Start by defining the
following:
Now type
PROPFRAC(G(X)). Note
that PROPFRAC can be
found on the POLYNOMIAL
submenu of the MATH
menu.
Pressing yields the
result shown at the right.
Solution 2
Enter the integral:
.
Pressing yields the
result shown at the right:
Pressing again
yields:
Working by hand:
, so:
Then, integrating term by term between 0 and 2
produces:
that is, since :
gx() 2
1
x 2+
------------
–=
Igx()xd
0
2
∫
=
2x 3+2x 2+()1–= gx() 2
1
x 2+
------------
–=
gx()x 2xx2+()ln–[]=d
0
2
∫
x 2=
x 0=
422ln=ln
gx()x 42ln–=d
0
2
∫
hp40g+.book Page 27 Friday, December 9, 2005 12:27 AM