Sharp EL-5060

– E-11 –
Differential/Integral Functions
Differential and integral calculations are only available in the
normal mode. For calculation conditions such as the x value in
differential calculation or the initial point in integral calculation,
only numerical values can be entered and equations such as 2
2
cannot be specified. It is possible to reuse the same equation
over and over again and to recalculate by only changing the
conditions without re-entering the equation.
• Performing a calculation will clear the value in the X memory.
•
When performing a differential calculation, enter the formula first
and then enter the x value in differential calculation and the minute
interval (dx). If a numerical value is not specified for minute inter-
val,
x ≠0 will be | x |×10
–5
and x =0 will be 10
–5
from the value of the
numeric derivative.
• When performing an integral calculation, enter the formula
first and then enter a range of integral (a, b) and subintervals
(n). If a numerical value is not specified for subintervals,
calculation will be performed using n=100.
Since differential and integral calculations are performed based
on the following equations, correct results may not be obtained,
in certain rare cases, when performing special calculations that
contain discontinuous points.
Integral calculation (Simpson’s rule):
S=—h{ƒ(a)+4{ƒ(a+h)+ƒ(a+3h)+······+ƒ(a+(N–1)h)}
+2{ƒ(a+2h)+ƒ(a+4h)+······+ƒ(a+(N–2)h)}+f(b)}
Differential calculation:
[When performing integral calculations]
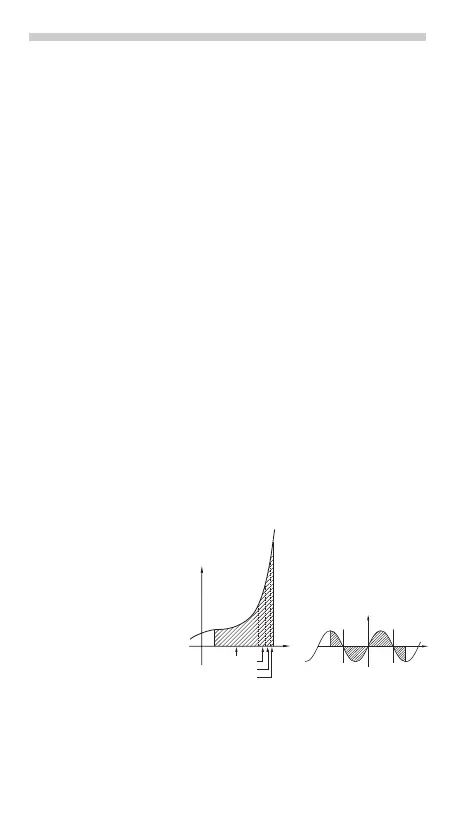
Integral calculations, de-
pending on the integrands
and subintervals included,
require longer calculation
time. During calculation,
“Calculating!” will be dis-
played. To cancel calcula-
tion, press ª. Note that
there will be greater inte-
gral errors when there are
large fluctuations in the integral values during minute shifting of the
integral range and for periodic functions, etc., where positive and
negative integral values exist depending on the interval.
For the former case, divide integral intervals as small as possi-
ble. For the latter case, separate the positive and negative val-
ues.
f(x+ ––)–f(x– ––)
dx
2
dx
2
f’(x)=————————
dx
1
3
N=2n








h=
b – a
N
a≤x≤b
——
y
x
b
xx
xx
a
0
13
2
y
a
b
x
x
x
x
x
1
0
2
3
EL5060E_En0616.pm65 06/16/2004, 13:1011