Rockwell Automation Publication 750-AT006D-EN-P - January 2022 11
Chapter 1 Background
10:902 [Load Coupling] – This parameter reflects the type of mechanical coupling between the motor and load. It adjusts calculated control
loop gains during an autotune bandwidth calculation test.
• 10:902 [Load Coupling] = Rigid (0) is where the load consists of few mechanical components with direct connection to the motor
shaft. The components are high performance, have no flex or twist, and misalignment is not likely to occur. This setting is used for
high-performance machines.
• 10:902 [Load Coupling] = Compliant (1) is a non-rigid load where position misalignment, backlash, and flexing of couplings, gearboxes,
belts, and shafts can occur which creates an indirect connection of the load to the motor shaft. This setting is common for most
machines. This is the default setting for Load Coupling.
Backlash
Backlash is the result of a small space between two mechanical components in a drive train, where they are not always in direct contact.
Backlash is caused by small geometric variations, manufacturing tolerances, and misalignments that are common in couplings, gearboxes,
linkages, and other mechanical components.
In gearboxes, it is a small space between two inter-meshing gear teeth.
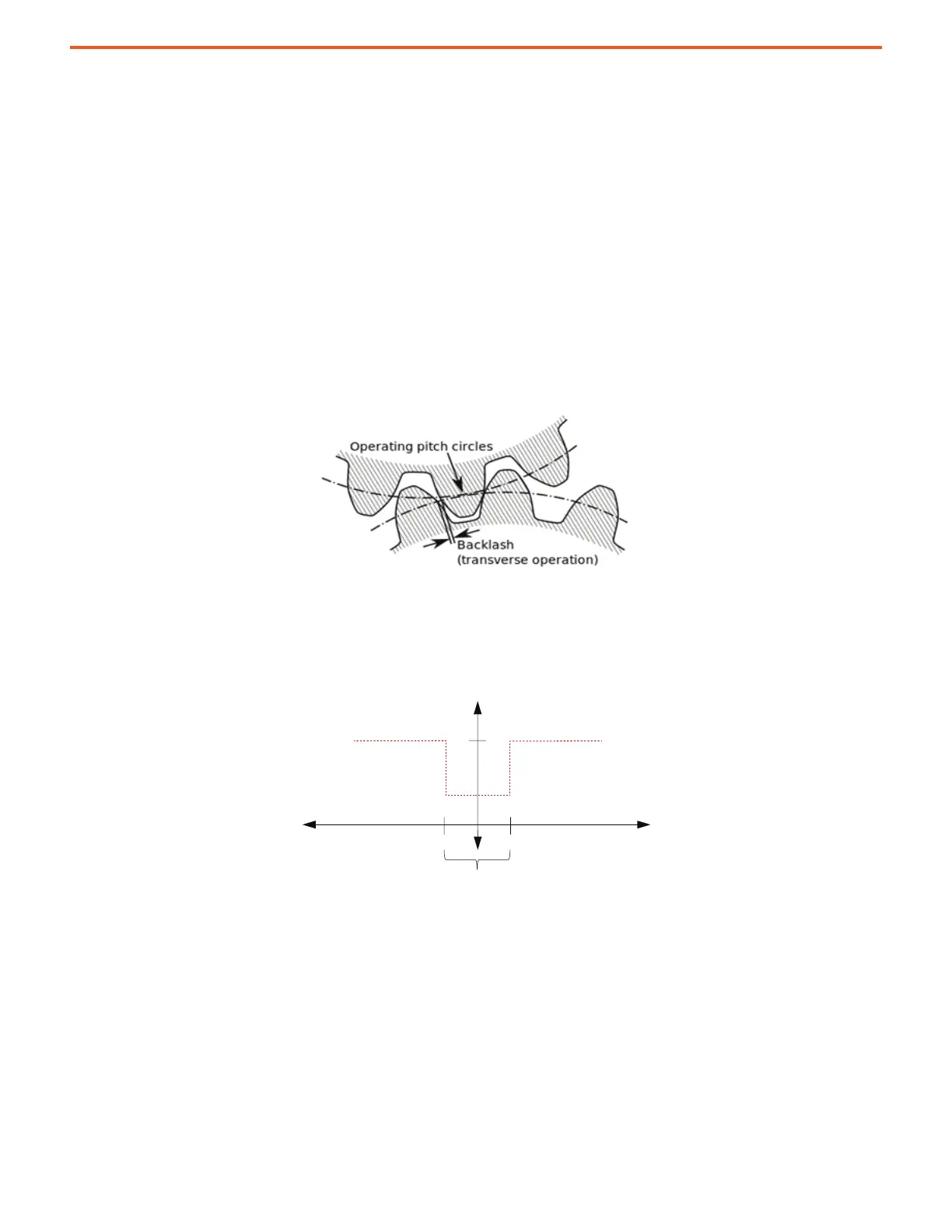
Figure 5 - Backlash in Gears
When the gears are not in contact and motor torque is applied, the input gear momentarily moves without transferring torque to the load.
Here, the total inertia driven by the motor is J
M
. When the gears come in contact, torque is then transferred to the load. Here, the total inertia
driven by the motor is J
T
. As a result, the effect of backlash is an instantaneous position-dependent step in total inertia.
Figure 6 - Backlash Effect
A similar problem exists in ballscrews where rotary motion is converted to linear motion. Ballscrews are often internally preloaded to reduce
backlash at the expense of added friction.
Another method of minimizing the effect of backlash in positioning applications is to always approach the target position from a forward
direction. When moving in reverse direction, the target position is surpassed and then a direction reversal is done. The target position is
then reached from the forward direction. This method cancels the effect of backlash distance and confirms that the final load side position
is consistent, regardless of where the starting load side position was.
This nonlinearity creates tuning problems in the form of resonances. A dynamic model is given.
Position
Inertia
Backlash Distance
J
M
J
T

 Loading...
Loading...