32 Math Functions
:expReg ae^(bx)
Fits the model equation y=a e^(bx) to the data
using least squares fit on linearised data for at
least two data points. It displays values for a and
b; it also displays values for r
2
and r.
% u " displays the DISTR menu, which has the following distribution
functions:
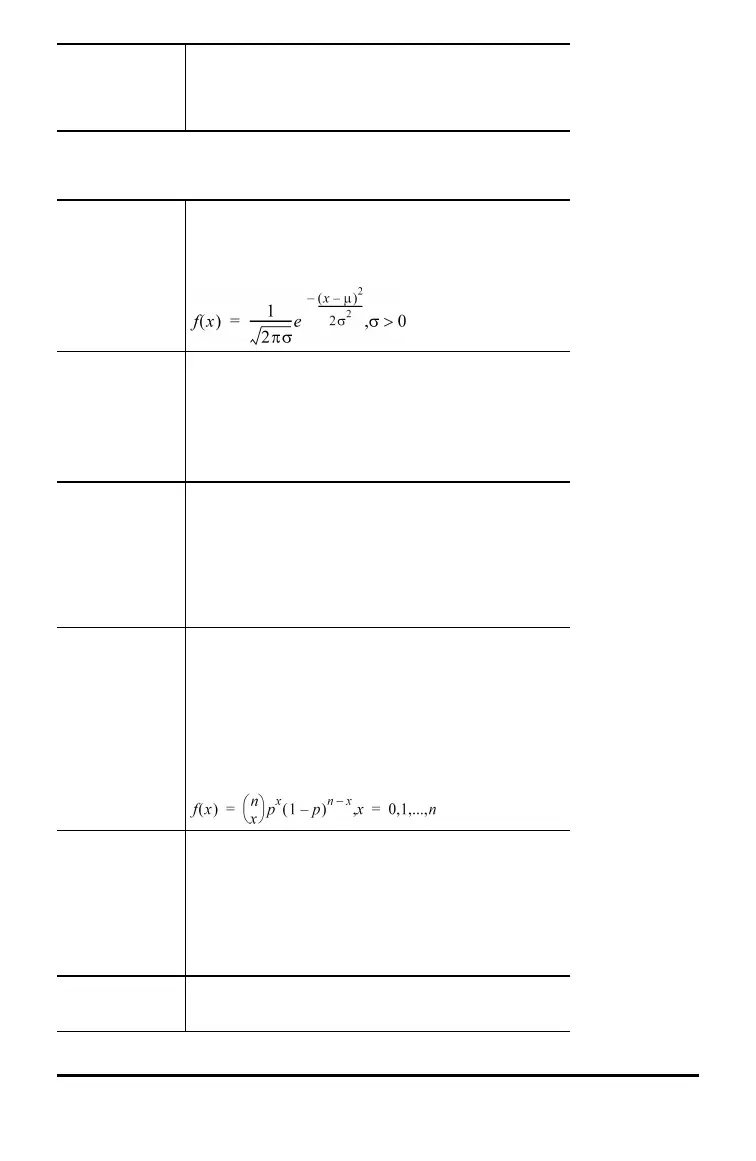
1:Normalpdf Computes the probability density function (pdf) for
the normal distribution at a specified x value. The
defaults are mean mu=0 and standard deviation
sigma=1. The probability density function (pdf) is:
2:Normalcdf Computes the normal distribution probability
between LOWERbnd and UPPERbnd for the
specified mean mu and standard deviation sigma.
The defaults are mu=0; sigma=1; with LOWERbnd
= M1E99 and UPPERbnd = 1E99.
Note: M1E99 to 1E99 represents Minfinity to infinity.
3:invNormal Computes the inverse cumulative normal
distribution function for a given area under the
normal distribution curve specified by mean mu
and standard deviation sigma. It calculates the x
value associated with an area to the left of the x
value. 0 { area { 1 must be true. The defaults are
area=1, mu=0 and sigma=1.
4:Binomialpdf Computes a probability at x for the discrete
binomial distribution with the specified numtrials
and probability of success (p) on each trial. x is a
non-negative integer and can be entered with
options of SINGLE entry, LIST of entries or ALL (list
of probabilities from 0 to numtrials is returned). 0
{ p { 1 must be true. The probability density
function (pdf) is:
5:Binomialcdf Computes a cumulative probability at x for the
discrete binomial distribution with the specified
numtrials and probability of success (p) on each
trial. x can be non-negative integer and can be
entered with options of SINGLE, LIST or ALL (a list
of cumulative probabilities is returned.) 0 { p { 1
must be true.
6:Poissonpdf Computes a probability at x for the discrete
Poisson distribution with the specified mean mu
 Loading...
Loading...











