2–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE
CHAPTER 2: ELECTRICAL BACKGROUND
In a three-phase, four-wire wye system it is necessary to use three elements. Three voltage
coils are connected between the three phases and the common neutral conductor. A
current coil is required in each of the three phases.
In modern digital meters, Blondell's Theorem is still applied to obtain proper metering. The
difference in modern meters is that the digital meter measures each phase voltage and
current and calculates the single-phase power for each phase. The meter then sums the
three phase powers to a single three-phase reading.
Some digital meters calculate the individual phase power values one phase at a time. This
means the meter samples the voltage and current on one phase and calculates a power
value. Then it samples the second phase and calculates the power for the second phase.
Finally, it samples the third phase and calculates that phase power. After sampling all three
phases, the meter combines the three readings to create the equivalent three-phase
power value. Using mathematical averaging techniques, this method can derive a quite
accurate measurement of three-phase power.
More advanced meters actually sample all three phases of voltage and current
simultaneously and calculate the individual phase and three-phase power values. The
advantage of simultaneous sampling is the reduction of error introduced due to the
difference in time when the samples were taken.
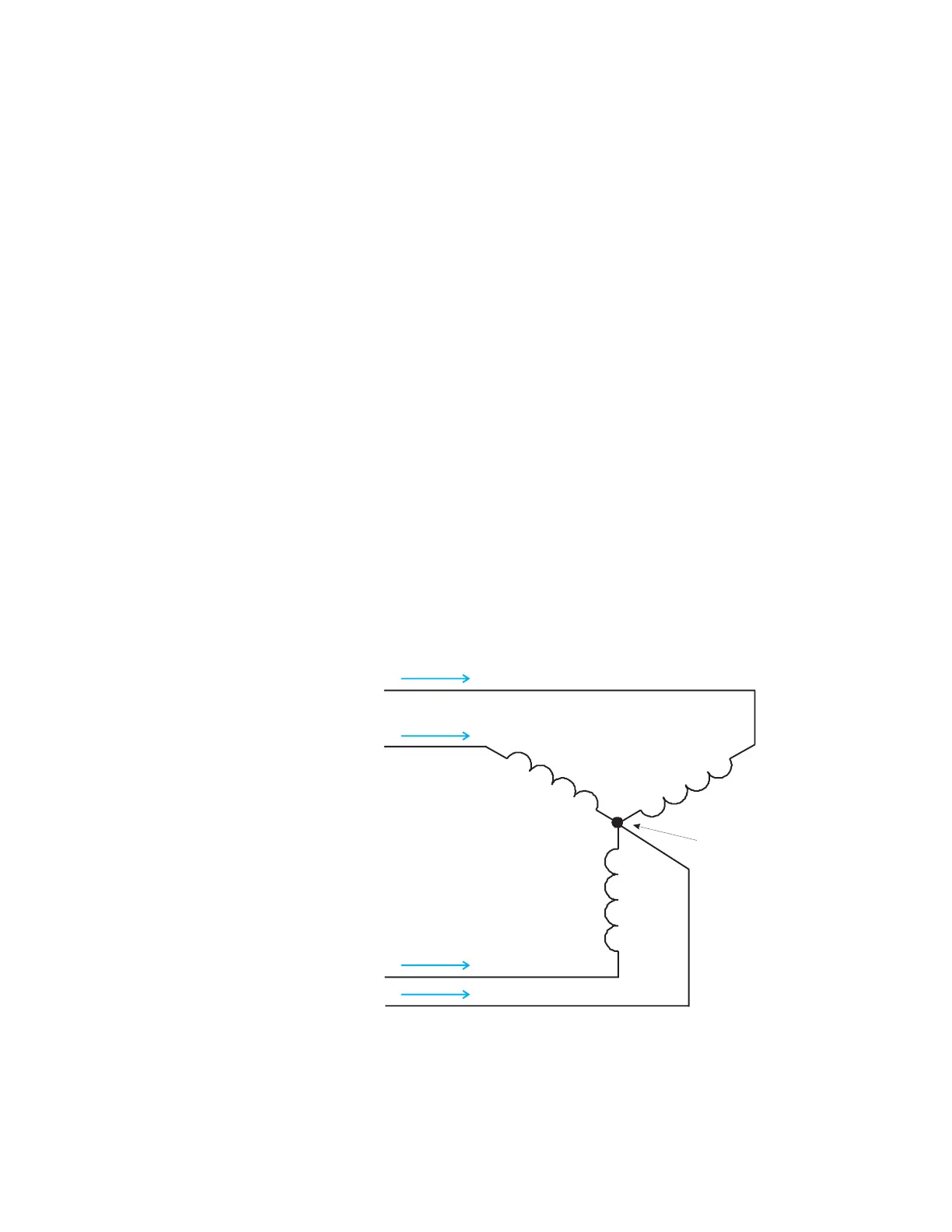
Blondell's Theorem is a derivation that results from Kirchhoff's Law. Kirchhoff's Law states
that the sum of the currents into a node is zero. Another way of stating the same thing is
that the current into a node (connection point) must equal the current out of the node. The
law can be applied to measuring three-phase loads. The figure below shows a typical
connection of a three-phase load applied to a three-phase, four-wire service. Kirchhoff's
Laws hold that the sum of currents A, B, C and N must equal zero or that the sum of
currents into Node “n” must equal zero.
FIGURE 2–6: Three-Phase Load Illustrating Kirchhoff’s Law and Blondell’s Theorem
Phase B
Phase C
Phase A
A
B
C
N
Node "n"

 Loading...
Loading...