HP Q METER 4342A - Q and Impedance Parameters; From Parallel and Series Measurements

Model 4342A
Section III
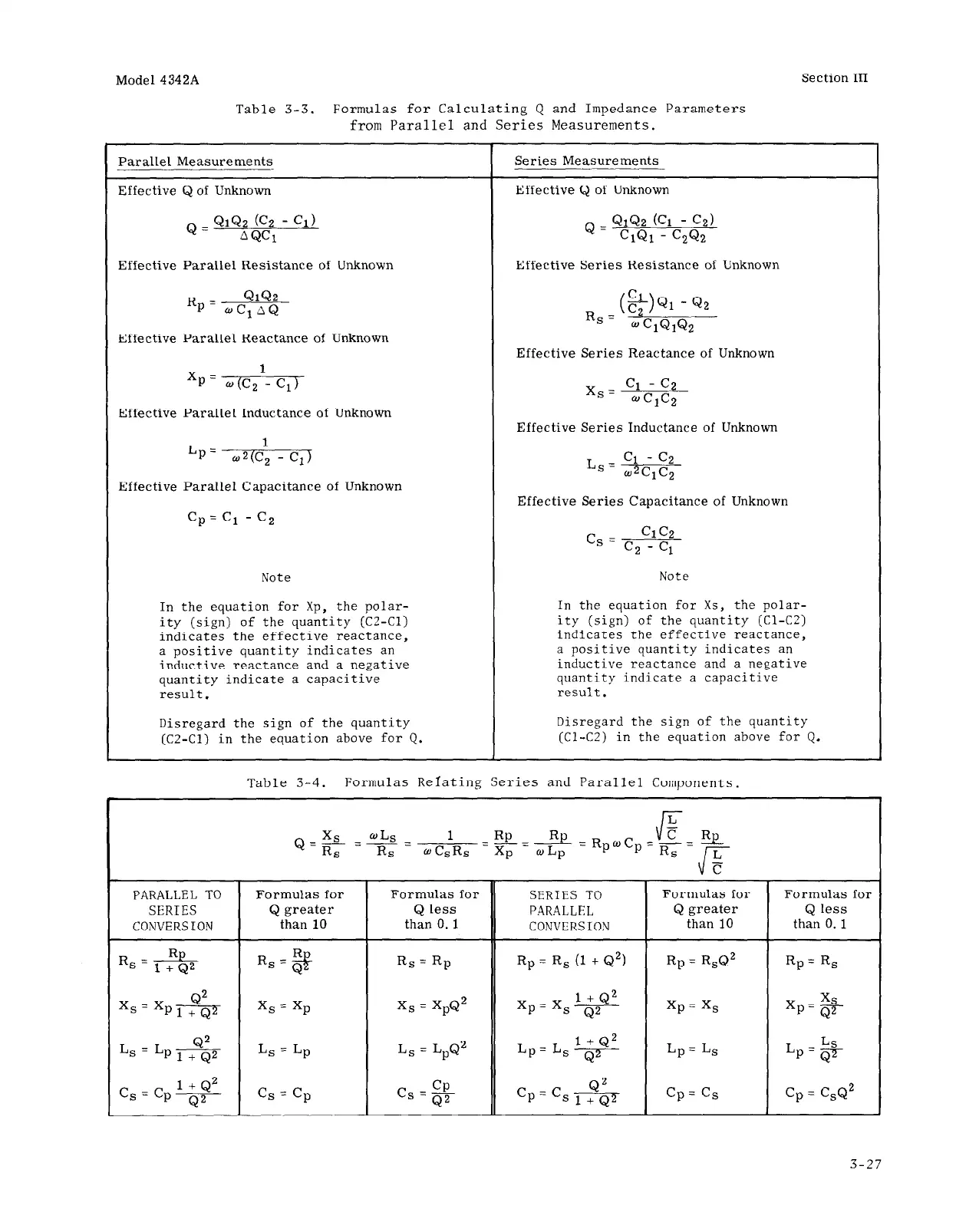
Table 3-3.
Formulas for Calculating Q and Impedance Parameters
from Parallel and Series Measurements.
Parallel Measurements
Effective Q of Unknown
Q = QlQ2 CC2 - Cl)
AQCl
Series Measurements
Effective Q of Unknown
Q = QIQZ (Cl - C2)
Cl&l - C2Q2
Effective Parallel Resistance of Unknown
Effective Series Resistance of Unknown
Rp =
QlQ2
oC,A&
R
S
= @Q1- Q2
w CIQIQZ
Effective Parallel Reactance of Unknown
Effective Series Reactance of Unknown
xp=
1
o(C, - Cl)
Effective Parallel Inductance of Unknown
x
S
_ Cl - C2
WClC2
Effective Series Inductance of Unknown
Lp=
1
w2(C2 - Cl)
Effective Parallel Capacitance of Unknown
cp=c, -c,
Note
In the equation for Xp, the polar-
ity (sign) of the quantity (CZ-Cl)
indicates the effective reactance,
a positive quantity indicates an
inductive reactance and a negative
quantity indicate a capacitive
result.
Disregard the sign of the quantity
(C2-Cl) in the equation above for Q.
L
S
= Cl - C2
W2ClC2
Effective Series Capacitance of Unknown
Cl C2
cs = c, - Cl
Note
In the equation for Xs, the polar-
ity (sign) of the quantity (Cl-C2)
indicates the effective reactance,
a positive quantity indicates an
inductive reactance and a negative
quantity indicate a capacitive
result.
Disregard the sign of the quantity
(Cl-C2) in the equation above for Q.
Table 3-4.
Formulas Relating Series and Parallel Components.
L
Q-e-““- l Rp=i!k=
ll-
Rs
wCsRs =xp
WLP
RpwCp+ =
S
L
r
c
PARALLEL TO
Formulas for Formulas for SERIES TO
Formulas for Formulas for
SERIES
Q greater Q less
PARALLEL
Q greater Q less
CONVERSION
than 10 than 0. 1
CONVERSION
than 10 than 0. 1
R, = -!fk
1 + Q2
Rs=g-
R, = Rp
Rp = R, (1 + Q2) Rp = RsQ2 Rp= R,
Q2
Xs=Xpl+Q2
x, = xp X, = XpQ2
xp= x&g xp= x,
xp=gf-
Q2
Ls = LP 1 + Q2
L, = Lp L, = LpQ2
1 +Q2
Lp=LsQ2
LP’ L,
Lp=$-
1 + Q2
‘, = ‘p Q2
cs = cp
cs = cp
Q2
Q2
cp=cs1+&2
cp= cs Cp = CsQ2