To Next Page

To Previous Page

Principles of Operation 9

effect to measure velocity fluctuations underwater, and can do so several times per second. But

exactly how does this transmission and receive of sound waves turn into velocity estimates?

Processing Technique

The phase difference between two transmit pulses is the basis for estimating current velocities using

the pulse coherent processing technique.

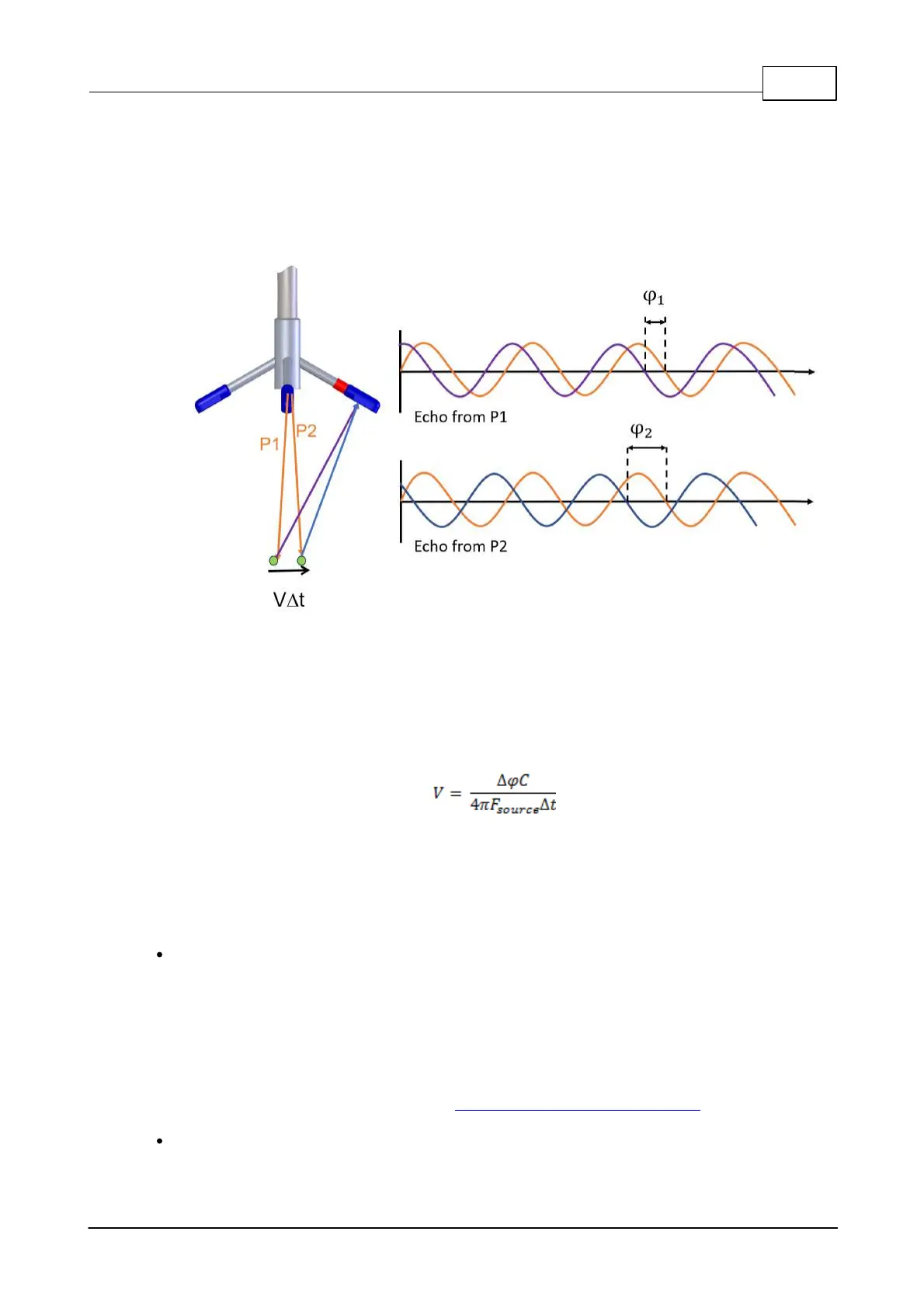
Figure: Tw o pulses are transmitted by the central transducer, w ith a tim e lag. The difference in phase

betw een the tw o transm it pulses is used to calculate velocity. The reflecting particle can be seen in

green, with a vector indicating its speed and direction

The phase difference between the two reflected pulses is a direct measure of the velocity, and can

be expressed as

Here, V is the current velocity, ∆φ is the phase difference, F_source is the transmitted frequency

and ∆t is the time difference between two consecutive pulses ("Lag"). The V is scaled with the speed

of sound in the liquid (C).

There are some aspects with the pulse coherent method that affects what the instrument is able to

measure.

The Doppler phase shift is computed using the covariance method. By computing the complex

covariance of the two return signals, the Doppler phase shift can be calculated by taking the four

quadrant arctangent (atan2 in most programming languages) of the real and imaginary parts of the

covariance function. This restricts solving the phase difference within the range of [-π, π]. The

calculation of φ is beyond the scope of this manual, but the impact of using this method is

important. It introduces the problem of ambiguous determination of the phase shift; if the phase

difference goes outside the range of ±π, the measurement uniqueness is lost, something known

as Velocity Ambiguity. For example, a sine wave with phase -π looks the same as a sine wave

with phase π. Read more about this here; Velocity Ambiguity and Phase Wrap, but the take home

is that there is a maximum velocity the instrument is able to measure.

The size of the lag (∆t in the equation above) determines the maximum unambiguous velocity that

can be measured. Longer lags have lower maximum velocities, while shorter lags have higher

maximum velocities. Conversely, longer lags will typically have higher velocity accuracy (lower

noise levels) than shorter lags, but potentially degraded signal correlation due to particle advection

Nortek Vectrino Comprehensive Manual

Other manuals for Nortek Vectrino