Theory of thermography
35
At room temperature (300 K) the peak of radiant emittance lies at 9.7 μm, in the far infra-
red, while at the temperature of liquid nitrogen (77 K) the maximum of the almost insignifi-
cant amount of radiant emittance occurs at 38 μm, in the extreme infrared wavelengths.
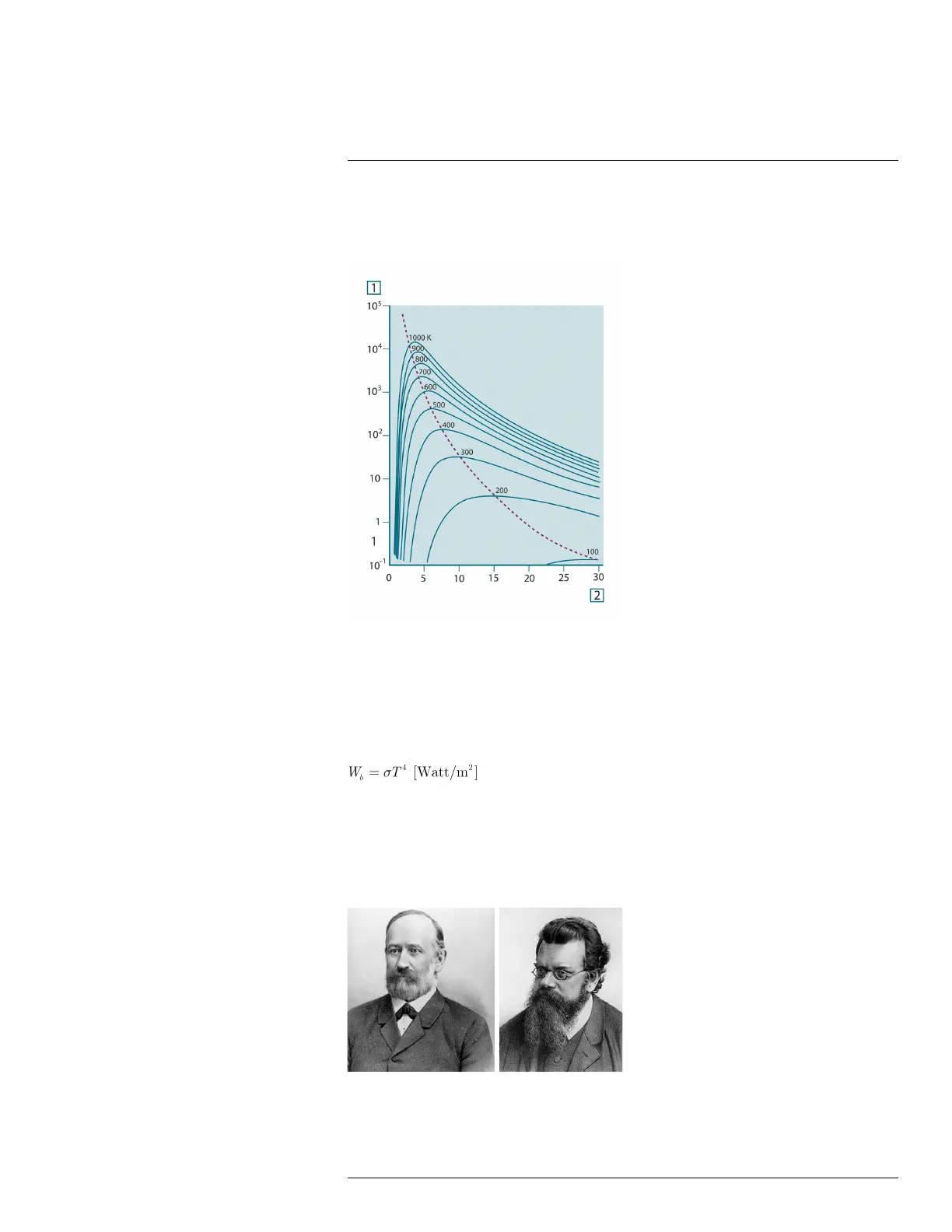
Figure 35.6 Planckian curves plotted on semi-log scales from 100 K to 1000 K. The dotted line represents
the locus of maximum radiant emittance at each temperature as described by Wien's displacement law. 1:
Spectral radiant emittance (W/cm
2
(μm)); 2: Wavelength (μm).
35.3.3 Stefan-Boltzmann's law
By integrating Planck’s formula from λ = 0 to λ = ∞, we obtain the total radiant emittance
(W
b
) of a blackbody:
This is the Stefan-Boltzmann formula (after Josef Stefan, 1835–1893, and Ludwig Boltz-
mann, 1844–1906), which states that the total emissive power of a blackbody is propor-
tional to the fourth power of its absolute temperature. Graphically, W
b
represents the area
below the Planck curve for a particular temperature. It can be shown that the radiant emit-
tance in the interval λ = 0 to λ
max
is only 25% of the total, which represents about the
amount of the sun’s radiation which lies inside the visible light spectrum.
Figure 35.7 Josef Stefan (1835–1893), and Ludwig Boltzmann (1844–1906)
#T810190; r. AI/41890/41890; en-US
243

 Loading...
Loading...