Cub Cadet 6X4 User Manual

Chapter 9 - Electrical
294
Electrical environment: AC Vs. DC
Most modern outdoor power equipment that has an
electrical system complex enough to require diagnosis
will be equipped with an alternator that produces alter-
nating current (AC). In most systems, this current is
immediately rectified to direct current (DC), and regu-
lated to a nominal 12 Volts. The presence of AC is
very limited.
The primary concern of this section is 12 Volt DC sys-
tems, though much of the theory and techniques apply
equally well to other DC systems.
1. Voltage: Pressure
• Voltage is the “pressure” that electricity has. It is
the amount of force pushing electrons through a
circuit.
• The unit of measurement for this pressure is
volts.
• The capital letter “V” is used to represent volts.
• Most (not all) outdoor power equipment operates
on a nominal 12 volts. In practice, system volt-
age may run as high as 13.5V or 14V.
2. Amperes: Flow
• Current is the “flow” of electricity. It is the amount
of electrons flowing in circuit.
• The flow of current is measured in Amperes or
Amps for short.
• The capital letter “I” is used to represent Amps.
3. Ohms: Resistance
• Resistance is the opposition to current flow. It is
a restriction that slows down the flow of current.
• Resistance is measured in Ohm’s.
• The greek letter omega “
Ω”, or the letter ”R” for
Resistance
is used to represent Ohm’s.
• Resistance creates heat. A circuit with too much
electrical load, or too much resistance for the
load placed on it will get hot.
4. Ohm’s Law: relates voltage, amperage, and
resistance
• Ohm’s law states that voltage is the product of
resistance times current.
• It is written as V = I x R.
• In simplest terms, it goes like this:
It takes 1 volt to push 1 amp through a resis-
tance of 1 ohm (1 = 1 x 1).
• This equation can be rearranged using algebra
to solve for any one variable.
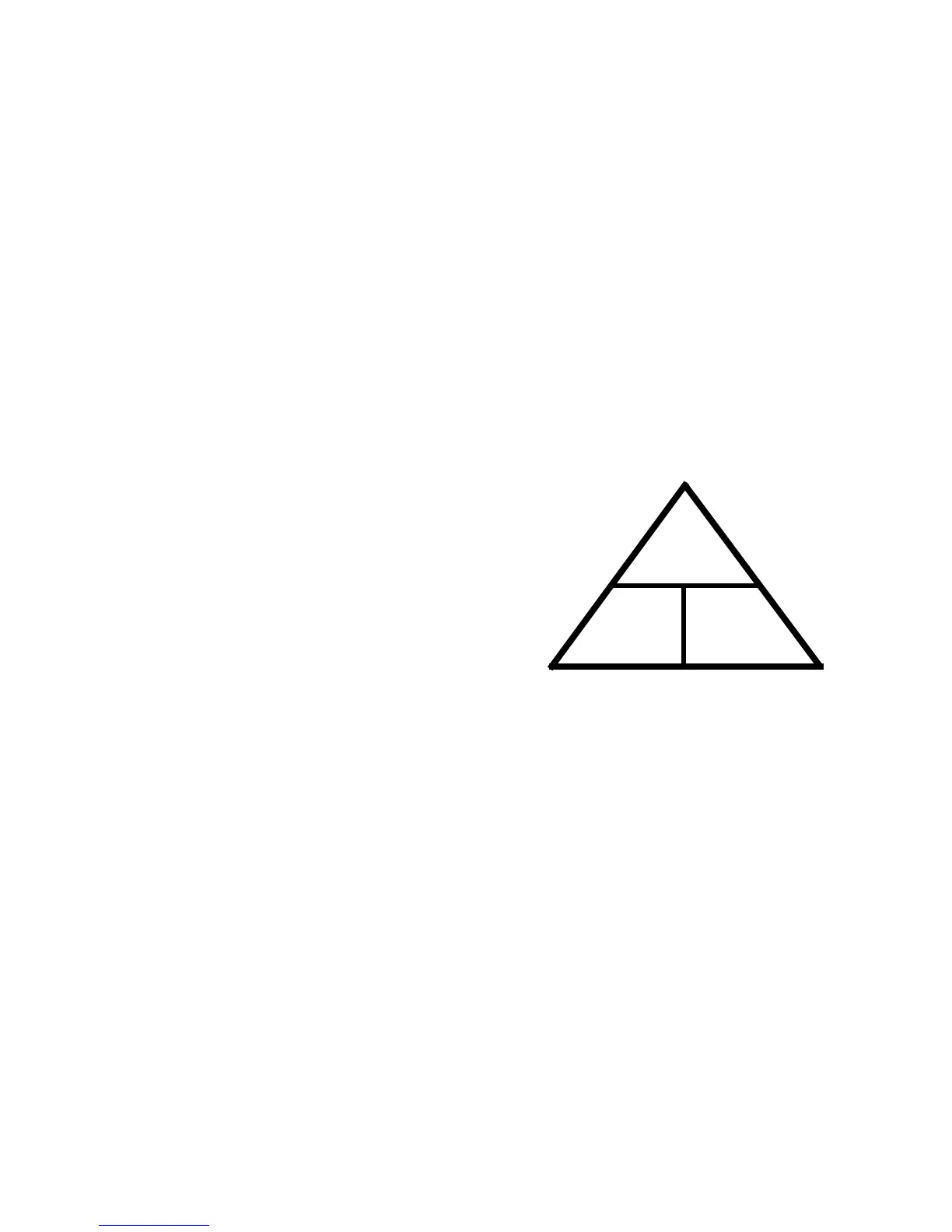
• Those who were traumatized by algebra can
represent Ohm’s law as a triangle.
When using the triangle, cover the value to be
found, and the two values left exposed signify
how to obtain that value. See Figure 9.44.
• As an example if the “R” is covered, the “V” is
over the “I” which means “V” divided by ”I” will
solve for the covered letter “R” (V/I = R).
If the “V” is covered, “I” and “R” are exposed on
the same line, meaning that the sum of “I” times
“R” will solve for the unknown “V” (I x R = V).
Figure 9.44
V
I
R

Cub Cadet 6X4 Specifications

General

Brand	Cub Cadet
Model	6X4
Category	Utility Vehicle
Language	English